题目内容
我区某中学为丰富学生的校园生活,准备从军跃体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元,根据的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买 个篮球.
考点:一元一次不等式的应用
专题:
分析:先设一个篮球a元,一个足球b元,根据购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元,列方程组求出a、b的值,然后设这所中学购买x个篮球,(96-x)个足球,根据购买足球和篮球的总费用不超过5720元,列不等式求出最大整数解.
解答:解:设一个篮球a元,一个足球b元,
由题意得,
,
解得:
,
即一个篮球80元,一个足球50元,
设这所中学购买x个篮球,(96-x)个足球,
由题意得,80x+(96-x)×50≤5720,
解得:x≤
,
则这所中学最多可以购买30个篮球.
故答案为:30.
由题意得,
|
解得:
|
即一个篮球80元,一个足球50元,
设这所中学购买x个篮球,(96-x)个足球,
由题意得,80x+(96-x)×50≤5720,
解得:x≤
| 92 |
| 3 |
则这所中学最多可以购买30个篮球.
故答案为:30.
点评:本题考查了一元一次不等式和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出题目中的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
相关题目
在如图形中若∠l=∠2,则可以使AB∥CD的是( )
A、 |
B、 |
C、 |
D、 |
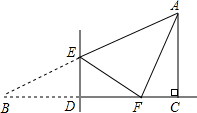 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=9.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 如图,在△ABC中,点D是BC的中点,DA⊥AC,tan∠BAD=
如图,在△ABC中,点D是BC的中点,DA⊥AC,tan∠BAD=