题目内容
“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和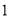 个过滤网要花费
个过滤网要花费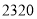 元,买
元,买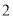 个空气净化器和
个空气净化器和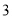 个过滤网要花费
个过滤网要花费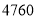 元.
元.
(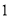 )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(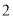 )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买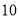 个空气净化器和
个空气净化器和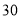 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目


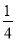 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的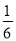 ,求道路的宽.
,求道路的宽.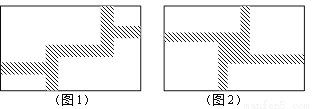
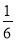 ,列方程求解即可.
,列方程求解即可.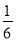 ×20×12,
×20×12,
 中的x和y都扩大2倍,那么分式的值( )
中的x和y都扩大2倍,那么分式的值( )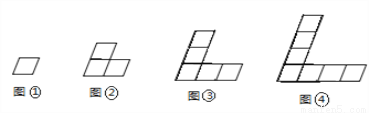
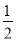 .
.