题目内容
 如图,点D是等腰直角三角形ABC的直角边BC上一点,AD的垂直平分线分别交AC、AD、AB于点E、O、F.且BC=1.
如图,点D是等腰直角三角形ABC的直角边BC上一点,AD的垂直平分线分别交AC、AD、AB于点E、O、F.且BC=1.(1)若AD是边BC上的中线,求AE的值;
(2)若四边形AEDF是菱形,求CD的值.
考点:菱形的性质,线段垂直平分线的性质,等腰直角三角形
专题:
分析:(1)根据线段垂直平分线上的点到两端点的距离相等AE=DE,设AE=DE=x,再表示出CE,根据线段中点的定义表示出CD,然后在Rt△CDE中,利用勾股定理列出方程求解即可;
(2)根据菱形的对边平行可得DE∥AB,然后根据两直线平行,同位角相等可得∠CDE=∠B=45°,从而判断出△CDE是等腰直角三角形,根据等腰直角三角形的性质可得CD=CE,设CD=x,表示出AE,再根据菱形的四条边都相等可得DE=AE,然后在Rt△CDE中,利用勾股定理列出方程求解即可.
(2)根据菱形的对边平行可得DE∥AB,然后根据两直线平行,同位角相等可得∠CDE=∠B=45°,从而判断出△CDE是等腰直角三角形,根据等腰直角三角形的性质可得CD=CE,设CD=x,表示出AE,再根据菱形的四条边都相等可得DE=AE,然后在Rt△CDE中,利用勾股定理列出方程求解即可.
解答:解:(1)∵EF垂直平分AD,
∴AE=DE,
设AE=DE=x,
∵△ABC是等腰直角三角形,
∴AC=BC=1,
∴CE=AC-AE=1-x,
∵AD是边BC上的中线,
∴CD=
BC=
,
在Rt△CDE中,CE2+CD2=DE2,
即(1-x)2+(
)2=x2,
解得x=
,
即AE=
;
(2)∵△ABC是等腰直角三角形,
∴AC=BC=1,∠B=45°,
∵四边形AEDF是菱形,
∴DE∥AB,
∴∠CDE=∠B=45°,
∴△CDE是等腰直角三角形,
∴CD=CE,
设CD=x,则AE=1-x,
∵四边形AEDF是菱形,
∴DE=AE=1-x,
在Rt△CDE中,CE2+CD2=DE2,
即x2+x2=(1-x)2,
整理得,x2+2x-1=0,
解得x1=
-1,x2=-
-1(舍去),
∴CD的值是
-1.
∴AE=DE,
设AE=DE=x,
∵△ABC是等腰直角三角形,
∴AC=BC=1,
∴CE=AC-AE=1-x,
∵AD是边BC上的中线,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△CDE中,CE2+CD2=DE2,
即(1-x)2+(
| 1 |
| 2 |
解得x=
| 5 |
| 8 |
即AE=
| 5 |
| 8 |
(2)∵△ABC是等腰直角三角形,
∴AC=BC=1,∠B=45°,
∵四边形AEDF是菱形,
∴DE∥AB,
∴∠CDE=∠B=45°,
∴△CDE是等腰直角三角形,
∴CD=CE,
设CD=x,则AE=1-x,
∵四边形AEDF是菱形,
∴DE=AE=1-x,
在Rt△CDE中,CE2+CD2=DE2,
即x2+x2=(1-x)2,
整理得,x2+2x-1=0,
解得x1=
| 2 |
| 2 |
∴CD的值是
| 2 |
点评:本题考查了菱形的性质,线段垂直平分线上的点到两端点的距离相等的性质,等腰直角三角形的性质,熟记性质并表示出△CDE的三边,然后利用勾股定理列出方程是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°,
如图,在四边形ABCD中,∠A=∠BCD=90°,∠B=45°, 如图是一块蛋糕,表面的形状是平行四边形,且内有一个平行四边形的孔.你能一刀将它切成面积相等的两块吗?请说出你的切法,并画出示意图.
如图是一块蛋糕,表面的形状是平行四边形,且内有一个平行四边形的孔.你能一刀将它切成面积相等的两块吗?请说出你的切法,并画出示意图. 如图,E是线段AC上的一点,AB⊥EB于B,AD⊥ED于D,且∠1=∠2,CB=CD,求证:∠3=∠4.
如图,E是线段AC上的一点,AB⊥EB于B,AD⊥ED于D,且∠1=∠2,CB=CD,求证:∠3=∠4.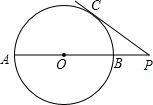 如图,AB是⊙O的直径,P是AB延长线上的一点,PC切⊙O于点C.若PC=6,PB=2,则⊙O的半径是
如图,AB是⊙O的直径,P是AB延长线上的一点,PC切⊙O于点C.若PC=6,PB=2,则⊙O的半径是 如图,在正方形ABCD中,以CD为边向外作等边△CDE,则∠AED=
如图,在正方形ABCD中,以CD为边向外作等边△CDE,则∠AED= 如图,在平面直角坐标系中.已知点A(3,0),B(-1,0),C(0,2),则以A,B,C为顶点的平行四边形的第四个顶点D的坐标为
如图,在平面直角坐标系中.已知点A(3,0),B(-1,0),C(0,2),则以A,B,C为顶点的平行四边形的第四个顶点D的坐标为