题目内容
18.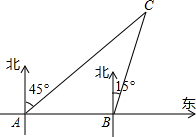 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
分析 过点B作BD⊥AC于D,由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,则可求得∠ACB的度数,然后利用三角函数的知识求解即可求得答案.
解答 解:过点B作BD⊥AC于D.
由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,
∴∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,BD=AB•sin∠BAD=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$(海里),
在Rt△BCD中,BC=$\frac{BD}{sin∠BCD}$=$\frac{10\sqrt{2}}{\frac{1}{2}}$=20$\sqrt{2}$(海里).
答:此时船C与船B的距离是20$\sqrt{2}$海里.
点评 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某校调查在校七年级学生的身高,在七年级学生中随机抽取35名学生进行了调查,具体数据如下:
可估算出该校七年级学生的平均身高为160.8cm.
| 身高(cm) | 158 | 159 | 160 | 161 | 162 | 163 |
| 人数(个) | 6 | 3 | 6 | 6 | 5 | 9 |
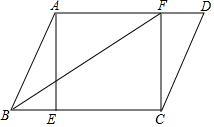 如图,在平行四边形ABCD中,过点A作AE⊥BC交BC边于点E,点F在边AD上,且DF=BE.
如图,在平行四边形ABCD中,过点A作AE⊥BC交BC边于点E,点F在边AD上,且DF=BE. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.