题目内容
5.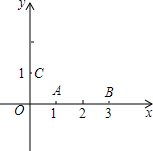 如图,已知点A(1,0)、B(3,0)、C(0,1).
如图,已知点A(1,0)、B(3,0)、C(0,1).(1)若二次函数图象经过点A、C和点D(2,$-\frac{1}{3}$)三点,求这个二次函数的解析式.
(2)求∠ACB的正切值.
(3)若点E在线段BC上,且△ABE与△ABC相似,求出点E的坐标.
分析 (1)根据点C的坐标,设抛物线y=ax2+bx+1,将点A、D的坐标代入,求出a、b的值,可得出二次函数的解析式;
(2)过点B作CA垂线交CA的延长线于点M,易知Rt△AMB为等腰直角三角形,然后过点M作MN⊥x轴,垂足为N,可得OA=AN=NB=1,继而证得Rt△OAC≌Rt△NAM,求出∠ACB的正切值;
(3)要使△ABE与△ABC相似,需AB2=BE•BC,然后代入求出BE的长度,过点E作EF⊥x轴,垂足为F,根据三角函数的知识求出EF、OF的长度,继而求出OF的长度,得出点E的坐标.
解答 解:(1)点C的坐标为(0,1),设抛物线y=ax2+bx+1,
将点A、D的坐标代入得:$\left\{\begin{array}{l}{a+b+1=0}\\{4a+2b+1=-\frac{1}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=\frac{1}{3}\\ b=-\frac{4}{3}.\end{array}\right.$,
故所求解析式为:y=$\frac{1}{3}$x2-$\frac{4}{3}$x+1;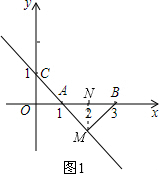
(2)过点B作CA垂线交CA的延长线于点M,如图1所示,
易知Rt△AMB为等腰直角三角形,
故有AM=MB,
过点M作MN⊥x轴,垂足为N,则OA=AN=NB=1,
则Rt△OAC≌Rt△NAM,故有CA=AM=MB,
故tan∠ACB=$\frac{MB}{CM}$=$\frac{1}{2}$;
(3)∵点A、B、C的坐标分别为(1,0)、(3,0)、(0,1).
若△ABE∽△ABC,则AB2=BE•BC,
∵AB=2,BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,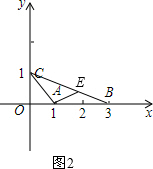
∴BE=$\frac{A{B}^{2}}{BC}$=$\frac{4}{\sqrt{10}}$,
过点E作EF⊥x轴,垂足为F,如右图2所示,
则EF=BE•sin∠EBF=$\frac{4}{\sqrt{10}}$×$\frac{1}{\sqrt{10}}$=$\frac{2}{5}$,
BF=BE•cos∠EBF=$\frac{4}{\sqrt{10}}$×$\frac{3}{\sqrt{10}}$=$\frac{6}{5}$,
OF=OB-BF=$\frac{9}{5}$,
∴点E的坐标为($\frac{9}{5},\frac{2}{5}$).
点评 本题考查了二次函数的综合应用,涉及了待定系数法确定函数关系式、全等三角形的判定与性质、勾股定理的应用、相似三角形的性质、三角函数的知识等知识点,综合性较强,难度适中.

 名校课堂系列答案
名校课堂系列答案| A. | (4,-2)或(-5,2) | B. | (4,-2)或(-4,-2) | C. | (4,2)或(-4,2) | D. | (4,2)或(-1,2) |
 如图,抛物线y=ax2+bx+c经过点(-1,4),与直线y=-x+1相交于A、B两点,其中点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,O).点M是直线AB上方的抛物线上一动点,过M作MP⊥x轴,垂足为点P,交直线AB于点N.设点M的横坐标为m.
如图,抛物线y=ax2+bx+c经过点(-1,4),与直线y=-x+1相交于A、B两点,其中点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,O).点M是直线AB上方的抛物线上一动点,过M作MP⊥x轴,垂足为点P,交直线AB于点N.设点M的横坐标为m.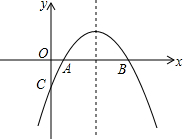 如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)
如图抛物线y=-x2+bx+c与x轴的两个交点别为A(1,0),B(3,0)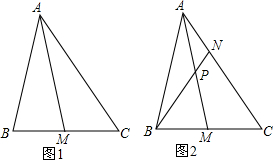
 已知:AC平分∠DAB,∠DAB+∠DCB=180°,若CE:CB=5:6,则S△ABD:S△CDB=$\frac{11}{25}$.
已知:AC平分∠DAB,∠DAB+∠DCB=180°,若CE:CB=5:6,则S△ABD:S△CDB=$\frac{11}{25}$.