��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������y=x2+bx+c��x�ύ��A��B���㣬��A��x��ĸ����ᣬ��B��x��������ᣬ��y�ύ�ڵ�C����CO=2AO��CO=BO��AB=3���������ж�����ȷ���ǣ�������


A���������ߵĽ���ʽΪy=x2+x��2
B����x��0ʱ��y����x�����������
C���ڴ��������ϵ�ij��M��ʹ��MAB���������5�������ĵ㹲������
D������������ֱ��y=��
 ֻ��һ������
ֻ��һ������
��
D�����㡿��������x��Ľ��㣮
����������ȷ��A��B������꣬������ý���ʽ��������߽���ʽ�����ǿɶ�Aѡ������жϣ����ݶ��κ��������ʶ�Bѡ������жϣ���M��t��t2��t��2�������������������ʽ�õ�
 ��3��|t2��t��2|=5���ٰѷ��̻�Ϊt2��t��2=
��3��|t2��t��2|=5���ٰѷ��̻�Ϊt2��t��2=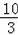
 ��t2��t��2=��
��t2��t��2=��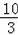
 ��Ȼ��ͨ������������ȷ��t��ֵ���Ӷ��ɶ�Cѡ������жϣ�ͨ���ⷽ��x2��x��2=��
��Ȼ��ͨ������������ȷ��t��ֵ���Ӷ��ɶ�Cѡ������жϣ�ͨ���ⷽ��x2��x��2=��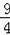
 �ɶ�Dѡ������жϣ�
�ɶ�Dѡ������жϣ�
����𡿽⣺��CO=2AO��CO=BO��AB=3��
��OA=1��OB=2��
��A����1.0����B��2��0����
�������߽���ʽΪy=��x+1����x��2������y=x2��x��2������Aѡ�����
�������ߵĶԳ���Ϊֱ��x=
 ��
��
�൱x��
 ʱ��y����x���������������Bѡ�����
ʱ��y����x���������������Bѡ�����
��M��t��t2��t��2����
����MAB���������5����
 ��3��|t2��t��2|=5��
��3��|t2��t��2|=5��
��t2��t��2=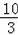
 ��t2��t��2=��
��t2��t��2=��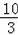
 ��
��
�߷���t2��t��2=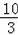
 ����������ʵ���⣬�����̻�t2��t��2=��
����������ʵ���⣬�����̻�t2��t��2=��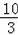
 û��ʵ���⣬
û��ʵ���⣬
������������M����2��������Cѡ�����
��y=��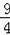
 ʱ��x2��x��2=��
ʱ��x2��x��2=��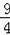
 �����x1=x2=
�����x1=x2=

����������ֱ��y=��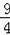
 ֻ��һ�����㣬����Dѡ����ȷ��
ֻ��һ�����㣬����Dѡ����ȷ��
��ѡD��
�����������⿼������������x��Ľ��㣺������κ���y=ax2+bx+c��a��b��c�dz�����a��0����x��Ľ�������ת��Ϊ�����x��һԪ���η��̣�Ҳ�����˸����б�ʽ����ϵ���Ĺ�ϵ�����ڶ��κ���y=ax2+bx+c��a��b��c�dz�����a��0������=b2��4ac������������x��Ľ����������=b2��4ac��0ʱ����������x����2�����㣻��=b2��4ac=0ʱ����������x����1�����㣻��=b2��4ac��0ʱ����������x��û�н��㣮

 ʮ��λ)��
ʮ��λ)��
 =0����y��0ʱ��m��ȡֵ��Χ����
=0����y��0ʱ��m��ȡֵ��Χ����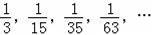
 �����˹���������ȥ���������еĵ�7��������
�����˹���������ȥ���������еĵ�7��������
 ����a+2b��2=a2��4b2
����a+2b��2=a2��4b2
 ʱ������Ķ���ʽ��ֵ��
ʱ������Ķ���ʽ��ֵ��




 B��
B��


 ������C(2��3)��ֱ��y��kx��b���������ཻ��A��B���㣬��ACB��90��
������C(2��3)��ֱ��y��kx��b���������ཻ��A��B���㣬��ACB��90�� ��
�� )��ֱ��д��ֱ��AB�Ľ���ʽ ��ȡ��B(4��﹣3)��ֱ��д��AB�Ľ���ʽΪ
)��ֱ��д��ֱ��AB�Ľ���ʽ ��ȡ��B(4��﹣3)��ֱ��д��AB�Ľ���ʽΪ 
