题目内容
按如图所示的方法折纸,下面结论正确的个数( )
①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.


A.1个 B.2个 C.3个 D.4个
C
【考点】翻折变换(折叠问题);相似三角形的判定与性质.
【分析】根据翻折变换的性质、相似三角形的判定定理解答即可.
【解答】解:由翻折变换的性质可知,∠AEB+∠FEC=
 ×180°=90°,
×180°=90°,
则∠AEF=90°,即∠2=90°,①正确;
由图形可知,∠1<∠AEC,②错误;
∵∠2=90°,
∴∠1+∠3=90°,又∠1+∠BAE=90°,
∴∠BAE=∠3,④正确;
∵∠BAE=∠3,∠B=∠C=90°,
∴△ABE∽△ECF,③正确.
故选:C.
【点评】本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目






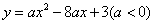 与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧. ,求△ABG的面积.
,求△ABG的面积.
 .
.