题目内容
按一定规律排列的一列数依次为: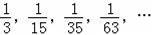
 ,按此规律排列下去,这列数中的第7个数是
,按此规律排列下去,这列数中的第7个数是

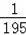
 .
.
【考点】规律型:数字的变化类.
【分析】首先根据题意,可得每个数的分子都是1;然后根据第一个数的分母3=1×3=(2×1﹣1)×(2×1+1),第二个数的分母15=3×5=(2×2﹣1)×(2×2+1),第三个数的分母35=5×7=(2×3﹣1)×(2×3+1),第四个数的分母63=7×9=(2×4﹣1)×(2×4+1),…,可得第n个数的分母是2n﹣1与2n+1的乘积,据此求出这列数中的第7个数的分母是多少,进而求出它的值是多少即可.
【解答】解:每个分数的分子都是1,
因为3=1×3=(2×1﹣1)×(2×1+1),
15=3×5=(2×2﹣1)×(2×2+1),
35=5×7=(2×3﹣1)×(2×3+1),
63=7×9=(2×4﹣1)×(2×4+1),
…,
所以第n个数的分母是2n﹣1与2n+1的乘积,
所以这列数中的第7个数是:
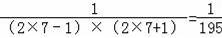
 .
.
故答案为: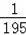
 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,BC=8,则AC等于( )
,BC=8,则AC等于( ) C.10 D.12
C.10 D.12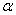 为锐角,则
为锐角,则 ﹦1﹣sin
﹦1﹣sin ,必有
,必有 .
. ,则有
,则有 .
.


 B.
B.

 D.
D.





 只有一个交点
只有一个交点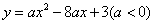 与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧. ,求△ABG的面积.
,求△ABG的面积.
 ,则
,则 的值是 。
的值是 。