题目内容
定义:如果一个y与x的函 数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:
数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如: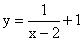
 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到
 的图象,则
的图象,则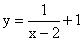
 是y与x的“反比例平移函数”.
是y与x的“反比例平移函数”.
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加x(cm)、y(cm)后,得到的新矩形的面积为8cm2,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”.
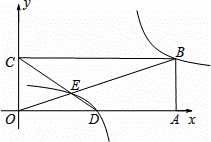
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”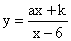
 的图象经过B、E两点.则这
的图象经过B、E两点.则这 个“反比例平移
个“反比例平移 函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.

(1)
 ,是;(2)
,是;(2)
 ,
,
 ;(3)(7,5)或(15,
;(3)(7,5)或(15,
 ).
).
【解析】

(2)把B和D的坐标代入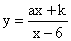
 得:
得:
 ,解得:
,解得:
 .
.
则“反比例平移函数”的表达式为
 .
.
故变换后的反比例函数表达式为
 .
.

当点P在点B右侧时,同理可得点P的坐标为(15,
 ).
).
综上所述,点P的坐标为(7,5)或(15,
 ).
).


考点:1.反比例函数综合题;2.新定义;3.平移的性质;4.转换思想和分类思想的应用.

练习册系列答案
相关题目
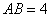
 ,点
,点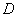
 的坐标是
的坐标是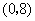
 ,以点
,以点
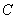
 为顶点的抛物线
为顶点的抛物线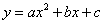
 经过
经过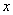
 轴上的点
轴上的点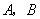
 .
.

 的坐标;
的坐标;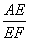
 =3,求
=3,求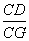

 :
: 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.

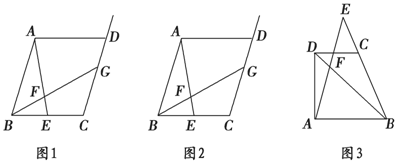
 在Rt△ABC中,∠C=900,∠B=300,BC=
在Rt△ABC中,∠C=900,∠B=300,BC=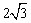 ,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直
,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直 线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为 。
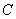
 :
:
 的顶点在坐标轴上.
的顶点在坐标轴上.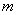
 的值;
的值;
 时,抛物线
时,抛物线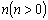
 个单位后与抛物线
个单位后与抛物线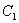
 :
: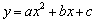
 关于
关于
 轴对称,且
轴对称,且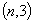
 ,求
,求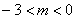
 时,抛物线
时,抛物线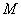
 ,且过点
,且过点
 .问在直线
.问在直线
 上是否存在一点
上是否存在一点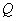
 使得△
使得△
 的周长最小,如果存在,求出点
的周长最小,如果存在,求出点 ,小正方形的边长为2
,小正方形的边长为2 的速度向大正方形的内部沿直线平移,设平移的时间为
的速度向大正方形的内部沿直线平移,设平移的时间为 秒,两个正方形重叠部分的面积为
秒,两个正方形重叠部分的面积为
 ,完成下列问题:
,完成下列问题: 含
含 ,求重叠部分的面积
,求重叠部分的面积

 AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
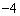 )两点。
)两点。
 C中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线
C中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线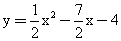 经过
经过 A、B两点。若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点
A、B两点。若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点 P,连结PA、P
P,连结PA、P B.设直线l移动的时间为t(0<t<4
B.设直线l移动的时间为t(0<t<4 )秒,求四
)秒,求四 边形PBCA的面积S(面
边形PBCA的面积S(面 积单
积单 位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积。
位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积。