题目内容
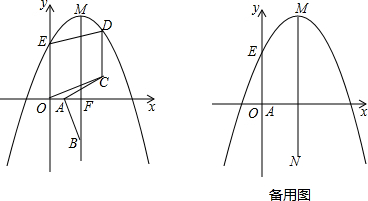
如图,抛物线y=-
x2+bx+3与y轴相交于点E,抛物线对称轴x=2交抛物线于点M,交x轴于点F,点A在x轴上,A(
,0),B(2,m)是射线FN上一动点,连结AB,将线段AB绕点A逆时针旋转90°得到线段AC,过点C作y轴的平行线交抛物线于点D.
(1)求b的值;
(2)求点C的坐标(用含m的代数式表示);
(3)当以O、E、D、C为顶点的四边形是平行四边形时,求点B的坐标.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求b的值;
(2)求点C的坐标(用含m的代数式表示);
(3)当以O、E、D、C为顶点的四边形是平行四边形时,求点B的坐标.

考点:二次函数综合题,解一元二次方程-公式法,全等三角形的判定与性质,平行四边形的性质
专题:综合题
分析:(1)只需运用抛物线的对称轴方程就可求出b的值;
(2)过点C作CH⊥x轴于H,易证△AFB≌△CHA,则有AF=CH,BF=AH,然后由A、B两点的坐标就可求出点C的坐标;
(3)由于DC∥OE,因此DC与OE是对边,则DC=OE,根据xD=xC即可求出点D的纵坐标(用m表示),然后只需分点D在点C的上方和下方两种讨论,根据DC=OE=3建立关于m的方程,并解这个方程,就可解决问题.
(2)过点C作CH⊥x轴于H,易证△AFB≌△CHA,则有AF=CH,BF=AH,然后由A、B两点的坐标就可求出点C的坐标;
(3)由于DC∥OE,因此DC与OE是对边,则DC=OE,根据xD=xC即可求出点D的纵坐标(用m表示),然后只需分点D在点C的上方和下方两种讨论,根据DC=OE=3建立关于m的方程,并解这个方程,就可解决问题.
解答:解:(1)由抛物线对称轴x=2得:
x=-
=b=2,
即b的值为2;
(2)过点C作CH⊥x轴于H,如图所示.
∵线段AC是由线段AB绕点A逆时针旋转90°所得,
∴AC=AB,∠CAB=90°,
∴∠CAF+∠BAF=90°.
∵BF⊥AF,AH⊥CH,
∴∠AHC=∠BFA=90°,∠BAF+∠ABF=90°,
∴∠CAF=∠ABF.
在△AFB和△CHA中,
,
∴△AFB≌△CHA(AAS),
∴AF=CH,BF=AH,
∵B(2,m),∴F(2,0).
∵B(2,m)是射线FN上一动点,∴m≤0,
∴AH=BF=-m.
∵A(
,0),∴OA=
,
∴CH=AF=OF-OA=2-
=
,OH=OA+AH=
-m,
∴点C的坐标为(
-m,
);
(3)当以O、E、D、C为顶点的四边形是平行四边形时,
∵抛物线y=-
x2+bx+3与y轴相交于点E,
∴E(0,3),OE=3.
∵CD∥y轴,即CD∥OE,
∴CD与OE是平行四边形的对边,
∴CD=OE=3.
∵CD∥y轴,
∴xD=xC=
-m,
∴yD=-
(
-m)2+2(
-m)+3=-
m2-
m+
.
①当点D在点C上方时,
CD=yD-yC═-
m2-
m+
-
=3,
整理得:4m2+12m+5=0,
解得:m1=-
,m2=-
,
∴点B的坐标为(2,-
)或(2,-
).
②当点D在点C下方时,
CD=yC-yD═
-(-
m2-
m+
)=3,
整理得:4m2+12m-43=0,
解得:m3=
,m4=
,
∵m<0,∴m=
,
∴点B的坐标为(2,
).
综上所述:符合条件的点B的坐标为(2,-
)或(2,-
)或(2,
).
x=-
| b | ||
2×(-
|
即b的值为2;
(2)过点C作CH⊥x轴于H,如图所示.
∵线段AC是由线段AB绕点A逆时针旋转90°所得,
∴AC=AB,∠CAB=90°,
∴∠CAF+∠BAF=90°.
∵BF⊥AF,AH⊥CH,
∴∠AHC=∠BFA=90°,∠BAF+∠ABF=90°,
∴∠CAF=∠ABF.
在△AFB和△CHA中,
|

∴△AFB≌△CHA(AAS),
∴AF=CH,BF=AH,
∵B(2,m),∴F(2,0).
∵B(2,m)是射线FN上一动点,∴m≤0,
∴AH=BF=-m.
∵A(
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=AF=OF-OA=2-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴点C的坐标为(
| 1 |
| 2 |
| 3 |
| 2 |
(3)当以O、E、D、C为顶点的四边形是平行四边形时,
∵抛物线y=-
| 1 |
| 2 |
∴E(0,3),OE=3.
∵CD∥y轴,即CD∥OE,
∴CD与OE是平行四边形的对边,
∴CD=OE=3.
∵CD∥y轴,
∴xD=xC=
| 1 |
| 2 |
∴yD=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 31 |
| 8 |
①当点D在点C上方时,
CD=yD-yC═-
| 1 |
| 2 |
| 3 |
| 2 |
| 31 |
| 8 |
| 3 |
| 2 |
整理得:4m2+12m+5=0,
解得:m1=-
| 1 |
| 2 |
| 5 |
| 2 |
∴点B的坐标为(2,-
| 1 |
| 2 |
| 5 |
| 2 |
②当点D在点C下方时,
CD=yC-yD═
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 31 |
| 8 |
整理得:4m2+12m-43=0,
解得:m3=
-3+2
| ||
| 2 |
-3-2
| ||
| 2 |
∵m<0,∴m=
-3-2
| ||
| 2 |
∴点B的坐标为(2,
-3-2
| ||
| 2 |
综上所述:符合条件的点B的坐标为(2,-
| 1 |
| 2 |
| 5 |
| 2 |
-3-2
| ||
| 2 |
点评:本题主要考查了抛物线的性质、旋转的性质、平行四边形的性质、全等三角形的判定与性质、解一元二次方程等知识,有一定综合性,构造全等三角形是解决第(2)小题的关键,分类讨论并利用CD=3建立等量关系是解决第(3)小题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、过A,B两点的直线长是A,B两点间的距离 |
| B、线段AB是A、B两点间的距离 |
| C、射线AB是A,B两点间的距离 |
| D、连接A,B两点的所有线中,线段AB的长度就是A,B两点间的距离 |
-3的相反数是( )
| A、3 | ||
B、
| ||
| C、-3 | ||
D、-
|
在直角坐标平面内,任意一个正比例函数的图象都经过点( )
| A、(1,1) |
| B、(1,0) |
| C、(0,1) |
| D、(0,0) |
 如图,△ABC的高AD、BE交于点F,求证:
如图,△ABC的高AD、BE交于点F,求证: 如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=
如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=