题目内容
10.如图,在某观测站A的正前方某海域B处有一艘船舶正向观测站驶来,并在观测站A测得俯角∠DAB=11°,10分钟后,该船舶到达C点,此时在观测站A测得俯角∠DAC=20°,已知观测站A距离海平面200米.求船舶的平均速度?(参考数据tan11°≈0.20,cos20°≈0.90,tan20°≈0.40)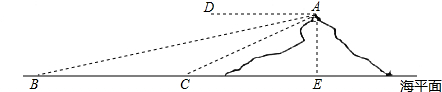
分析 根据速度=$\frac{路程}{时间}$,只要求出BC,在RT△ABE中求出BE,在RT△ACE中求出EC即可解决问题.
解答 解: 在RT△ABE中,∵∠AEB=90°,∠ABE=∠DAB=11°,AE=200,
在RT△ABE中,∵∠AEB=90°,∠ABE=∠DAB=11°,AE=200,
∴tan11°=$\frac{AE}{BE}$,
∴BE=$\frac{200}{0.20}$=1000,
在RT△ACE中,∵∠AEC=90°,∠ACE=∠DAC=20°,AE=200,
∴tan20°=$\frac{AE}{CE}$,
∴CE=$\frac{200}{0.4}$=500,
∴BC=BE-CE=1000-500=500,
∴船舶的平均速度为500÷$\frac{10}{60}$=3000米/小时=3千米/小时.
∴船舶的平均速度为3千米/小时.
点评 本题考查解直角三角形的应用,路程、速度、时间的关系等知识,解题的关键是记住锐角三角函数的定义,求出BE、CE的长,属于中考常考题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.上午9时30分,时钟的时针和分针所成的角为( )
| A. | 90° | B. | 100° | C. | 110° | D. | 105° |
19.下列等式成立的是( )
| A. | -22=2-2 | B. | -22=($\frac{1}{2}$)-2 | C. | (-2)-2=22 | D. | (-2)-2=($\frac{1}{2}$)2 |
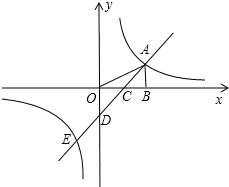 如图,在平面直角坐标系中,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
如图,在平面直角坐标系中,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.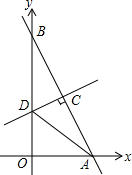 如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.
如图,在平面直角坐标系中,点A,B分别在x轴正半轴与y轴正半轴上,线段OA,OB(OA<OB)的长是方程x(x-4)+8(4-x)=0的两个根,作线段AB的垂直平分线交y轴于点D,交AB于点C.