题目内容
1.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(1)在图①中,画一个三角形,使它的三边长都是有理数.
(2)在图②中,画一个三角形,使它们的三边长分别是$\sqrt{5}$,$\sqrt{10}$,$\sqrt{17}$,并求出三角形的面积.

分析 (1)画直角边为3、4的直角三角形,由勾股定理可得斜边为5,即可得三边长都是有理数的三角形;
(2)由勾股定理得出$\sqrt{5}$、$\sqrt{10}$、$\sqrt{17}$,即可画出图形;用矩形的面积减去三个直角三角形的面积即可得出所求三角形的面积.
解答 解:(1)如图①,
∵AC=3,BC=4,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
故△ABC为所求作三角形;
(2)如图②,由勾股定理可知,
DE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,EF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,DF=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
∴△DEF为所求作三角形,
S△DEF=2×4-$\frac{1}{2}$×1×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=$\frac{7}{2}$.
点评 本题考查了勾股定理、三角形面积的计算方法;熟练掌握勾股定理,根据边长画出三角形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.先化简,再求值($\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{2-x}{x+2}$)÷$\frac{x}{x-2}$(其中x=3),其计算结果是( )
| A. | -$\frac{8}{5}$ | B. | 8 | C. | -8 | D. | $\frac{8}{5}$ |
9.若a+b=1,则a2-b2+2b的值为( )
| A. | 4 | B. | 3 | C. | 1 | D. | 0 |
10.若a>0且ax=2,ay=3,则ax-2y的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
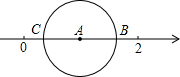 如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,则以点A为圆心,AB长为半径的圆交数轴于另一点C,则点C表示的数是2-$\sqrt{2}$.
如图,数轴上表示1、$\sqrt{2}$的对应点分别为A、B,则以点A为圆心,AB长为半径的圆交数轴于另一点C,则点C表示的数是2-$\sqrt{2}$. 在如图所示的△ABC中.
在如图所示的△ABC中.