题目内容
如图2 - 63所示,抛物线y=x2—2x-3与x轴交于A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求A,B两点的坐 标及直线AC的解析式;
标及直线AC的解析式;
(2)点P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值;
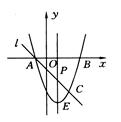
解:(1)令y=0,即x2—2x—3=0,解得x1=—1,x2=3,∴A(—l,0),B(3,0).将点C的横坐标x=2代入y=x2—2x—3,得y=—3,∴ C(2,—3),∴直线AC的解析式为y=—x-1. (2)设点P的横坐标为x(—1≤x≤2),则P,E的坐标分别为P(x,—x-1),E(x,x2—2x—3).∵点P在点E的上方,∴PE=—x—1—(x2—2x—3)=—(x—
C(2,—3),∴直线AC的解析式为y=—x-1. (2)设点P的横坐标为x(—1≤x≤2),则P,E的坐标分别为P(x,—x-1),E(x,x2—2x—3).∵点P在点E的上方,∴PE=—x—1—(x2—2x—3)=—(x— )2+
)2+ ,∴PE的最大
,∴PE的最大 值为
值为 .
.

练习册系列答案
相关题目
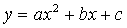 图象如图所示,则下列结论正确的( )
图象如图所示,则下列结论正确的( )