题目内容
4．
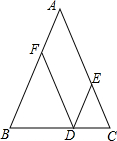如图，在△ABC中，AB=AC，点D在边BC上，过点D作DE∥AB与边AC交于点E、DF∥AC与边AB交于点F．（1）求证：四边形AFDE是平行四边形．
（2）若DE=2，DF=4，求AB的长．
分析 （1）由平行四边形的定义容易得出结论；
（2）由平行四边形的性质得出DE=AF．由等腰三角形的性质得出∠B=∠C．证出∠FDB=∠B，得出DF=BF，即可得出结果．
解答 （1）证明：∵DE∥AB，DF∥AC，
∴四边形AFDE是平行四边形．
（2）解：∵四边形AFDE是平行四边形，
∴DE=AF．
又∵AB=AC，
∴∠B=∠C．
又∵DF∥AC，
∴∠FDB=∠C．
∴∠FDB=∠B，
∴DF=BF．
∴AB=AF+BF=DE+DF=2+4=6．
点评 本题考查了平行四边形的判定与性质、等腰三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形是等腰三角形是解决（2）的关键．
练习册系列答案
相关题目
14．用公式法解一元二次方程${x^2}-\frac{1}{4}=2x$，正确的应是（ ）
| A． | $x=\frac{{-2±\sqrt{5}}}{2}$ | B． | $x=\frac{{2±\sqrt{5}}}{2}$ | C． | $x=\frac{{1±\sqrt{5}}}{2}$ | D． | $x=\frac{{1±\sqrt{3}}}{2}$ |
如图，在Rt△ABC中，∠ACB=90°，点D是边AB的中点，若AB=24，则CD的长是12．
9．
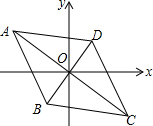如图，菱形ABCD的对角线相交于坐标原点，点A的坐标为（a，2），点B的坐标为（-1，-$\sqrt{3}$），点C的坐标为（2$\sqrt{3}$，c），那么a，c的值分别是（ ）
如图，菱形ABCD的对角线相交于坐标原点，点A的坐标为（a，2），点B的坐标为（-1，-$\sqrt{3}$），点C的坐标为（2$\sqrt{3}$，c），那么a，c的值分别是（ ）| A． | a=-1，c=-$\sqrt{3}$ | B． | a=-2$\sqrt{3}$，c=-2 | C． | a=1，c=$\sqrt{3}$ | D． | a=2$\sqrt{3}$，c=2 |
16．下列事件是随机事件的是（ ）
| A． | 晴天的早晨，太阳从东方升起 | |
| B． | 测量某天的最低气温，结果为-150℃ | |
| C． | 打开数学课本时刚好翻到第60页 | |
| D． | 在一次体育考试中，小王跑100米用了4秒钟 |
13．在9，$\sqrt{3}$，$\frac{3}{16}$，-0.1这四个数中，是无理数的是（ ）
| A． | 9 | B． | $\sqrt{3}$ | C． | $\frac{3}{16}$ | D． | -0.1 |