题目内容
14. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E为底AD上一点,将△ABE沿直线BE折叠,点A落在四边形对角线BD上的G处,EG的延长线交直线BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E为底AD上一点,将△ABE沿直线BE折叠,点A落在四边形对角线BD上的G处,EG的延长线交直线BC于点F.(1)写出图中所有的相似三角形(除全等外);
(2)选择其中的一对相似三角形,加以证明.
分析 (1)根据图形即可得到图中所有的相似三角形;
(2)根据两直线平行,内错角相等可得∠AEB=∠EBF,再根据折叠的性质可以判定出∠AEB=∠BEG,然后得到∠EBF=∠BEF,从而判断出△FEB为等腰三角形,再根据等角的余角相等求出∠ABG=∠EFB,然后根据等腰三角形的两个底角相等求出∠BAG=∠FBE,然后根据两角对应相等,两三角形相似,即可得到△ABG∽△BFE.
解答  解:(1)在不添加字母的情况下,图中所有的相似三角形:
解:(1)在不添加字母的情况下,图中所有的相似三角形:
△DAB∽△DGE∽△BGF,△ABG∽△BFE;
(2)选择:△ABG∽△BFE.
证明:∵AD∥BC,
∴∠AEB=∠EBF,
∵△EAB≌△EGB,
∴∠AEB=∠BEG,
∴∠EBF=∠BEF,
∴FE=FB,
∴△FEB为等腰三角形.
∵∠ABG+∠GBF=90°,∠GBF+∠EFB=90°,
∴∠ABG=∠EFB,
在等腰△ABG和△FEB中,∠BAG=(180°-∠ABG)÷2,∠FBE=(180°-∠EFB)÷2,
∴∠BAG=∠FBE,
∴△ABG∽△BFE.
点评 本题综合考查了相似三角形的性质与判定以及折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.解决问题的关键是掌握:有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
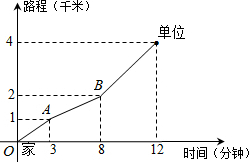 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是15分钟.
王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是15分钟. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOC的度数.
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOC的度数.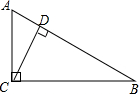 如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.