题目内容

20．如图，能判断直线AB∥CD的条件是（　　）
A．∠1=∠2B．∠3=∠4C．∠3+∠4=180°D．∠1+∠3=180°

分析 根据邻补角互补和条件，∠3+∠4=180°，可得∠3=∠5，再根据同位角相等两直线平行可得结论．

解答 解：∵∠4+∠5=180°，∠3+∠4=180°，
∴∠3=∠5，
∴AB∥CD，
故选C．

点评 此题主要考查了平行线的判定，关键是掌握同位角相等两直线平行．

练习册系列答案
相关题目
10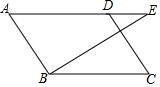．如图，?ABCD中，BE⊥AB于点B，交AD的延长线于点E，若CD=6，tan∠C=$\frac{4}{3}$，则BE=（　　）
A．10B．8C．6D．$\frac{9}{2}$
11．已知直线l1经过点A（1，0）与点B（3，2），另一条直线l2经过点C（2，-4），
（1）求直线l1的解析式；
（2）若直线l2与直线l1无交点，且与x轴交于点P，求P点坐标；
（3）已知点D（-2，1），判断A、C、D三点是否在同一条直线上．
8．正八边形的每一个内角的度数为（　　）
A．45°B．60°C．120°D．135°
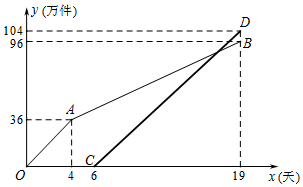15．爱贝玩具厂开发了一款新型益智玩具，一期计划生产200万件，预计20天后投入市场．该厂有甲、乙、丙三条生产线，由于丙生产线在技术创新升级中，则由甲、乙两条生产线先开始生产加工玩具．甲、乙两条生产线一起生产加工玩具4天后，乙生产线发生故障停止生产，只剩甲生产线单独加工玩具．为了能在规定时间完成任务，丙生产线加快了技术升级，6天后也投入生产．由于丙生产线技术升级后提高了效率，所以提前一天完成加工任务．已知甲、乙两条生产线生产玩具总量y1（万件）与时间x（天）的关系如图折线段OAB所示，丙生产线生产玩具总量y2（万件）与时间x（天）的关系如图线段CD所示．
（1）求第5天结束时，生产玩具总量．
（2）求玩具生产总量y（万件）与时间x（天）的函数关系式（注明x 的取值范围）．
（3）直接写出生产第几天时，甲、乙两条生产线生产玩具总量与丙生产线生产玩具总量差为20万件．
5．以下四个选项表示某天四个城市的平均气温，其中平均气温最低的是（　　）
A．-2B．5C．-10D．-5
12．若a与-2互为相反数，则a-1的值为（　　）
A．-3B．-$\frac{3}{2}$C．-$\frac{1}{2}$D．1
9．若代数式$\frac{1}{x+3}$在实数范围内有意义，则实数x的取值范围是（　　）
A．x=-3B．x≠-3C．x＜-3D．x＞-3
10．在平面直角坐标系中，直线y=x+3过点A，点B（2，0）和点C（m，2）在坐标平面内，若四边形AOBC为平行四边形，则m的值为1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网