题目内容
11.已知直线l1经过点A(1,0)与点B(3,2),另一条直线l2经过点C(2,-4),(1)求直线l1的解析式;
(2)若直线l2与直线l1无交点,且与x轴交于点P,求P点坐标;
(3)已知点D(-2,1),判断A、C、D三点是否在同一条直线上.
分析 (1)根据A、B两点坐标,利用待定系数法求解可得;
(2)由直线l2与直线l1无交点知直线l2∥直线l1,从而直线l2的解析式为y=x+m,利用点C的坐标可得直线l2的解析式,继而得出点P的坐标;
(3)待定系数法求得直线AC解析式,再判断点D是否在直线AC上即可.
解答 解:(1)设直线l1的解析式为y=kx+b,
将点A(1,0)、B(3,2)代入,得:
$\left\{\begin{array}{l}{k+b=0}\\{3k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
则直线l1的解析式为y=x-1;
(2)∵直线l2与直线l1无交点,
∴直线l2∥直线l1,
∴设直线l2的解析式为y=x+m,
将点C(2,-4)代入,得:2+m=-4,
解得:m=-6,
∴直线l2的解析式为y=x-6,
当y=0时,x-6=0,即x=6,
则点P的坐标为(6,0);
(3)设直线AC的解析式为y=ax+n,
将点A(1,0)、C(2,-4)代入,得:
$\left\{\begin{array}{l}{a+n=0}\\{2a+n=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-4}\\{n=4}\end{array}\right.$,
则直线AC的解析式为y=-4x+4,
当x=-2时,y=-4×(-2)+4=12≠1,
∴点D不在直线AC上,即A、C、D三点不在同一条直线上.
点评 本题主要考查两直线相交或平行的问题,熟练掌握两直线平行时自变量的系数相等及待定系数法求函数解析式是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
19.若反比例函数y=$\frac{k}{x}$(k<0)的图象经过点(-2,y1),(-1,y2),(2,y3),则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
3.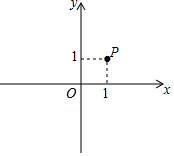 在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )
在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )
 在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )
在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )| A. | (1,-1) | B. | (-1,1) | C. | (3,1) | D. | (1,2) |
20. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠3+∠4=180° | D. | ∠1+∠3=180° |
1.下列计算正确的是( )
| A. | (2a-1)2=2a2-2a+1 | B. | (2a+1)2=4a2+1 | C. | (-a-1)2=-a2-2a+1 | D. | (2a-1)2=4a2-4a+1 |
 如图,直线y=x+2与双曲线y=$\frac{k}{x}$相交于点A,点A的纵坐标为3,则k的值为( )
如图,直线y=x+2与双曲线y=$\frac{k}{x}$相交于点A,点A的纵坐标为3,则k的值为( )


