题目内容
15.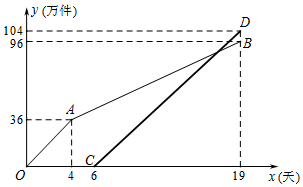 爱贝玩具厂开发了一款新型益智玩具,一期计划生产200万件,预计20天后投入市场.该厂有甲、乙、丙三条生产线,由于丙生产线在技术创新升级中,则由甲、乙两条生产线先开始生产加工玩具.甲、乙两条生产线一起生产加工玩具4天后,乙生产线发生故障停止生产,只剩甲生产线单独加工玩具.为了能在规定时间完成任务,丙生产线加快了技术升级,6天后也投入生产.由于丙生产线技术升级后提高了效率,所以提前一天完成加工任务.已知甲、乙两条生产线生产玩具总量y1(万件)与时间x(天)的关系如图折线段OAB所示,丙生产线生产玩具总量y2(万件)与时间x(天)的关系如图线段CD所示.
爱贝玩具厂开发了一款新型益智玩具,一期计划生产200万件,预计20天后投入市场.该厂有甲、乙、丙三条生产线,由于丙生产线在技术创新升级中,则由甲、乙两条生产线先开始生产加工玩具.甲、乙两条生产线一起生产加工玩具4天后,乙生产线发生故障停止生产,只剩甲生产线单独加工玩具.为了能在规定时间完成任务,丙生产线加快了技术升级,6天后也投入生产.由于丙生产线技术升级后提高了效率,所以提前一天完成加工任务.已知甲、乙两条生产线生产玩具总量y1(万件)与时间x(天)的关系如图折线段OAB所示,丙生产线生产玩具总量y2(万件)与时间x(天)的关系如图线段CD所示.(1)求第5天结束时,生产玩具总量.
(2)求玩具生产总量y(万件)与时间x(天)的函数关系式(注明x 的取值范围).
(3)直接写出生产第几天时,甲、乙两条生产线生产玩具总量与丙生产线生产玩具总量差为20万件.
分析 (1)根据函数图象及图象中的数据可以求得第5天结束时,生产玩具总量;
(2)根据题意可以分段求出玩具生产总量y(万件)与时间x(天)的函数关系式;
(3)根据题意可知在丙生产前它们相差20万件和生产后相差20万件两种情况,从而可以解答本题.
解答 解:(1)由题意可得,
甲的生产效率为:(96-36)÷(19-4)=4万件/天,
则第5天结束时的生产总量为:36+(5-4)×4=40(万件),
答:第5天结束时,生产玩具总量是40万件;
(2)当0≤x≤4时,设y与x的函数关系式为y=kx,
36=4k,得k=9,
即当0≤x≤4时,y与x的函数关系式为y=9x,
当4<x<6时,设y与x的函数关系式为y=ax+b,
$\left\{\begin{array}{l}{4a+b=36}\\{5a+b=40}\end{array}\right.$,得$\left\{\begin{array}{l}{a=4}\\{b=20}\end{array}\right.$,
即当4<x<6时,y与x的函数关系式为y=4x+20,
当6≤x≤19时,丙的工作效率是:104÷(19-6)=8万件/天,
将x=6代入y=4x+20中,得y=44,
则当6≤x≤19时,y与x的函数关系式为:y=(4+8)(x-6)+44=12x-28,
由上可得,y与x的函数关系式为:y=$\left\{\begin{array}{l}{9x}&{(0≤x≤4)}\\{4x+20}&{(4<x<6)}\\{12x-28}&{(6≤x≤19)}\end{array}\right.$;
(3)由题意可得,
将y=20代入y=9x,得x=$\frac{20}{9}$=2$\frac{2}{9}$,
设CD段对应的函数解析式为y=cx+d,
$\left\{\begin{array}{l}{6c+d=0}\\{19c+d=104}\end{array}\right.$,得$\left\{\begin{array}{l}{c=8}\\{d=-48}\end{array}\right.$,
即CD段对应的函数解析式为y=8x-48,
∴(4x+20)-(8x-48)=20,
解得,x=12,
∴在第3天和第12天甲、乙两条生产线生产玩具总量与丙生产线生产玩具总量差为20万件,
答:生产第3天和第12天时,甲、乙两条生产线生产玩具总量与丙生产线生产玩具总量差为20万件.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用一次函数的性质和数形结合的思想解答.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | ±$\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | $\sqrt{{(-3)}^{2}}$=-3 | D. | ±$\sqrt{4}$=2 |
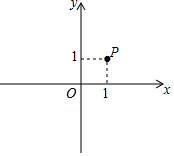 在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )
在平面直角坐标系xOy中,点P的坐标为(1,1).如果将x轴向上平移2个单位长度,y轴不变,得到新坐标系,那么点P在新坐标系中的坐标是( )| A. | (1,-1) | B. | (-1,1) | C. | (3,1) | D. | (1,2) |
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠3+∠4=180° | D. | ∠1+∠3=180° |
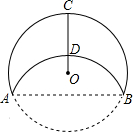 如图,将半径为12的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )
如图,将半径为12的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )| A. | 3$\sqrt{15}$ | B. | 4$\sqrt{15}$ | C. | 6$\sqrt{15}$ | D. | 12 |
| A. | a2•a3=a6 | B. | -a6•(-a)2=a8 | C. | (ab2)3=ab6 | D. | (-2a2)2=4a4 |
| A. | 扩大6倍 | B. | 扩大4倍 | C. | 扩大2倍 | D. | 不变 |
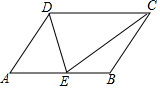 如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )
如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )