题目内容
20.阅读下列材料,解答下面的问题:我们知道方程2x+3y=12有无数个解,但在实际生活中我们往往只需求出其正整数解.
例:由2x+3y=12,得:y=$\frac{12-2x}{3}$=4-$\frac{2}{3}$x(x、y为正整数).要使y=4-$\frac{2}{3}$x为正整数,则$\frac{2}{3}$x为正整数,由2,3互质,可知:x为3的倍数,从而x=3,代入y=4-$\frac{2}{3}$x=2.所以2x+3y=12的正整数解为$\left\{\begin{array}{l}x=3\\ y=2\end{array}$
问题:
(1)请你直接写出方程3x-y=6的一组正整数解$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
(2)若$\frac{12}{x-3}$为自然数,则满足条件的正整数x的值有B个.
A.5 B.6 C.7 D.8
(3)七年级某班为了奖励学生学习的进步,购买为单价3元的笔记本与单价为5元的钢笔两种奖品,共花费48元,问有几种购买方案,写出购买方案?
分析 (1)求方程3x-y=6的正整数解,可给定x一个正整数值,计算y的值,如果y的值也是正整数,那么就是原方程的一组正整数解.
(2)参照例题的解题思路进行解答;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.则根据题意得:3m+5n=48,其中m、n均为自然数.解该二元一次方程即可.
解答 解:(1)由3x-y=6,得
y=3x-6,
要使y是正整数,则3x-6是正整数,所以需要x>2,
故当x=3时,y=3,
所以3x-y=6的一组正整数解可以是:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
故答案是:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$;
(2)若$\frac{12}{x-3}$是自然数,则满足条件的正整数x有4,5,6,7,9,15共6个,
故答案是:B;
(3)设购买单价为3元的笔记本m本,单价为5元的钢笔n支.
则根据题意得:3m+5n=48,其中m、n均为自然数.
于是有:n=$\frac{48-3m}{5}$,
则有:$\left\{\begin{array}{l}{\frac{48-3m}{5}>0}\\{m>0}\end{array}\right.$,
解得:0<m<16.
由于n=$\frac{48-3m}{5}$为正整数,则48-3m为正整数,且为5的倍数.
∴当m=1时,n=9;
当m=6时,n=6,
当m=11时,n=3.
答:有三种购买方案:即购买单价为3元的笔记本1本,单价为5元的钢笔9支;
或购买单价为3元的笔记本6本,单价为5元的钢笔6支;
或购买单价为3元的笔记本11本,单价为5元的钢笔3支.
点评 本题考查了二元一次方程的应用,解题关键是要读懂题目给出的已知条件,根据条件求解.注意笔记本和钢笔是整体,所有不可能出现小数和负数,这也就说要求的是正整数.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案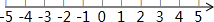 解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.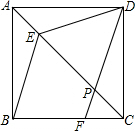 如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线于点P,且DE=DP.
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线于点P,且DE=DP.
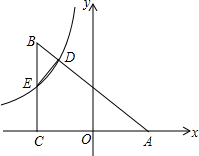 如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.
如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.