题目内容
已知，如图，点D为△ABC的边AB的中点，点E为AC上一点，AE=2CE，BE和CD相交于点O．求证：OE=| 1 |
| 4 |
考点：平行线分线段成比例
专题：证明题
分析：过E点作EF∥CD交AB于F，如图，根据平行线分线段成比例定理，由EF∥CD得到
=
=2，即AF=2DF，而D点为AB的中点，所以BD=AD=3DF，则BF=4DF，然后再根据平行线分线段成比例定理，由OD∥EF得到
=
=
，即有OE=
BE．
| AF |
| DF |
| AE |
| CE |
| DF |
| BF |
| OE |
| BE |
| 1 |
| 4 |
| 1 |
| 4 |
解答：证明：过E点作EF∥CD交AB于F，如图，
∵EF∥CD，
∴
=
=
=2，即AF=2DF，
∴AD=3DF，
∵D点为AB的中点，
∴BD=AD=3DF，
∴BF=4DF，
∵OD∥EF，
∴
=
=
，
∴OE=
BE．
∵EF∥CD，
∴
| AF |
| DF |
| AE |
| CE |
| 2CE |
| CE |
∴AD=3DF，
∵D点为AB的中点，
∴BD=AD=3DF，
∴BF=4DF，
∵OD∥EF，
∴
| DF |
| BF |
| OE |
| BE |
| 1 |
| 4 |
∴OE=
| 1 |
| 4 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，∠AOB=∠COD，则∠AOC与∠DOB的大小关系是（ ）| A、∠AOC＞∠DOB |
| B、∠AOC＜∠DOB |
| C、∠AOC=∠DOB |
| D、∠AOC与∠DOB无法比较大小 |
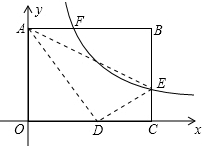矩形OABC在平面直角坐标系中如图，已知AB=10，BC=8，EB是C上一点，将△ABE沿AE折叠，点B刚好与OC边上点D重合，过点E的反比例函数y=
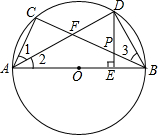如图，△ABC内接于⊙O，AB为直径，∠CAB的平分线交BC于点F，交⊙O于点D，DE⊥AB于点E，且交BC于点P，BF=
如图，在△ABC中，AD是BC边上的中线，sinB=