题目内容
6.点(a-1,y1)、(a+1,y2)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若y1<y2,则a的范围是-1<a<1.分析 根据反比例函数的性质分两种情况进行讨论,①当点(a-1,y1)、(a+1,y2)在图象的同一支上时,②当点(a-1,y1)、(a+1,y2)在图象的两支上时.
解答 解:∵k>0,
∴在图象的每一支上,y随x的增大而减小,
①当点(a-1,y1)、(a+1,y2)在图象的同一支上,
∵y1<y2,
∴a-1>a+1,
解得:无解;
②当点(a-1,y1)、(a+1,y2)在图象的两支上,
∵y1<y2,
∴a-1<0,a+1>0,
解得:-1<a<1,
故答案为:-1<a<1.
点评 此题主要考查了反比例函数的性质,关键是掌握当k>0时,在图象的每一支上,y随x的增大而减小.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
16.计算(-a3)2的结果是( )
| A. | a5 | B. | -a5 | C. | a6 | D. | -a6 |
18.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
 小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?
小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高? 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.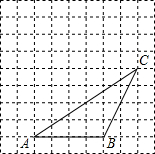 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.