题目内容
12. 如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x>0)经过Rt△AOB直角边AB上的三等分点C,与斜边OA相交于点M,则$\frac{OM}{OA}$=$\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$.
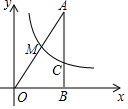
如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x>0)经过Rt△AOB直角边AB上的三等分点C,与斜边OA相交于点M,则$\frac{OM}{OA}$=$\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$.
分析 A(a,3b),M(m,n),则C(a,b)或(a,2b),作MN⊥OB于N.分两种情形求解即可.
解答 解:设A(a,3b),M(m,n),则C(a,b)或(a,2b),作MN⊥OB于N.
∵MN∥AB,
∴$\frac{ON}{OB}$=$\frac{MN}{AB}$=$\frac{OM}{OA}$,
∴$\frac{n}{3b}$=$\frac{m}{a}$,
∴n=$\frac{3bm}{a}$,
①当C(a,b)时,∵M、C在y=$\frac{k}{x}$上,
∴ab=$\frac{3b{m}^{2}}{a}$,
∴a=$\sqrt{3}$m,
∴$\frac{OM}{OA}$=$\frac{ON}{OB}$=$\frac{m}{\sqrt{3}m}$=$\frac{\sqrt{3}}{3}$,
②当C(a,2b)时,∵M、C在y=$\frac{k}{x}$上,
∴2ab=$\frac{3b{m}^{2}}{a}$,
∴a=$\frac{\sqrt{3}}{\sqrt{2}}$m,
∴$\frac{OM}{OA}$=$\frac{ON}{OB}$=$\frac{m}{\frac{\sqrt{3}}{\sqrt{2}}m}$=$\frac{\sqrt{6}}{3}$,
综上所述,$\frac{OM}{OA}$=$\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$或$\frac{\sqrt{6}}{3}$.
点评 本题考查反比例函数的应用、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会利用参数解决问题,属于中考常考题型.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.已知在五边形ABCDE中,∠A+∠B=240°,∠C+∠D=170°,则∠E的度数为( )
| A. | 30° | B. | 110° | C. | 120° | D. | 130° |




 如图,三个相同的三角尺拼接成一个图形,请找出图中的所有平行线,并写出完整推理说明平行的理由.
如图,三个相同的三角尺拼接成一个图形,请找出图中的所有平行线,并写出完整推理说明平行的理由.