题目内容
 如图,AB为⊙O的直径,D是BC延长线上的一点,OC的延长线交AD延长线于E点且DE=2,AD=4,EC=2
如图,AB为⊙O的直径,D是BC延长线上的一点,OC的延长线交AD延长线于E点且DE=2,AD=4,EC=2| 3 |
(1)试判断AE和⊙O的位置关系,并说明理由.
(2)求∠E的度数.
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)根据相似三角形的判定推出△ECD∽△EAC,推出∠ECD=∠EAC,求出∠B=∠DAC,推出∠BAD=90°,根据切线的判定推出即可;
(2)求出∠CAD=30°,推出∠B=∠CAD=∠BCO=∠ECD=30°,求出∠DCA=90°,根据三角形内角和定理求出即可.
(2)求出∠CAD=30°,推出∠B=∠CAD=∠BCO=∠ECD=30°,求出∠DCA=90°,根据三角形内角和定理求出即可.
解答:解:(1)AE和⊙O相切,
理由是:∵DE=2.,AD=4,EC=2
,
∴AE=DE+AD=6,
=
=
,
=
=
,
∴
=
,∠E=∠E,
∴△ECD∽△EAC,
∴∠ECD=∠EAC,
AB为⊙O的直径,
∴∠ACB=90°,
∵OA=OB,
∴∠B=∠BCO=∠ECD=∠EAC,
∵∠B+∠BAC=90°,
∴∠EAC+∠BAC=90°,
∴EA⊥OA,OA半径,
∴AE和⊙O相切;
(2)由(1)得:△ECD∽△EAC,
∴
=
=
,
∵∠ACD=180°-∠ACB=90°,
∴tan∠DAC=
=
,
∴∠DAC=30°
∴∠ECD=∠DAC═30°
∴∠E=180°-∠DAC-∠ECD-∠ACD=30°.
理由是:∵DE=2.,AD=4,EC=2
| 3 |
∴AE=DE+AD=6,
| DE |
| EC |
| 2 | ||
2
|
| ||
| 3 |
| EC |
| EA |
2
| ||
| 6 |
| ||
| 3 |
∴
| DE |
| EC |
| EC |
| EA |
∴△ECD∽△EAC,
∴∠ECD=∠EAC,
AB为⊙O的直径,
∴∠ACB=90°,
∵OA=OB,
∴∠B=∠BCO=∠ECD=∠EAC,
∵∠B+∠BAC=90°,
∴∠EAC+∠BAC=90°,
∴EA⊥OA,OA半径,
∴AE和⊙O相切;
(2)由(1)得:△ECD∽△EAC,
∴
| CD |
| AC |
| EC |
| EA |
| ||
| 3 |
∵∠ACD=180°-∠ACB=90°,
∴tan∠DAC=
| CD |
| AC |
| ||
| 3 |
∴∠DAC=30°
∴∠ECD=∠DAC═30°
∴∠E=180°-∠DAC-∠ECD-∠ACD=30°.
点评:本题考查了切线的判定,相似三角形的性质和判定,解直角三角形,等腰三角形的性质等知识点的应用,题目比较好,综合性比较强.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
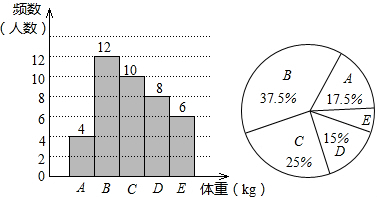 进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: