题目内容
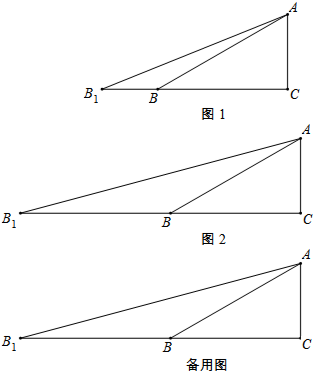 我们把“按照某种理想化的要求(或实际可能应用的标准)来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”(我国著名数学家徐利治).
我们把“按照某种理想化的要求(或实际可能应用的标准)来反映或概括的表现某一类或一种事物关系结构的数学形式”看作是一个数学中的一个“模式”(我国著名数学家徐利治).如图是一个典型的图形模式,用它可测底部可能达不到的建筑物的高度,用它可测河宽,用它可解决数学中的一些问题.等等.
(1)如图,若B1B=30米,∠B1=22°,∠ABC=30°,求AC(精确到1);
(参考数据:sin22°≈0.37,cos22°≈0.92,tan22°≈0.40,
| 3 |
(2)如图2,若∠ABC=30°,B1B=AB,计算tan15°的值(保留准确值);
(3)直接写出tan7.5°的值.(注:若出现双重根式
a+b
|
考点:解直角三角形的应用,勾股定理
专题:几何图形问题,压轴题,转化思想
分析:(1)在Rt△ABC和Rt△AB1C中,利用三角函数,用AC分别表示出BC和B1C,根据B1B=B1C-BC,列方程求得AC的长;
(2)设B1B=AB=x,在Rt△ABC中,利用三角函数用x表示出AC和BC的长,则B1C即可求得,根据正切的定义即可求解;
(3)按照(1)(2)的规律,画出含有7.5°角、15°角和30°角的直角三角形,如答图3所示,利用勾股定理、等腰三角形的性质及正切的定义,求出tan7.5°的值.
(2)设B1B=AB=x,在Rt△ABC中,利用三角函数用x表示出AC和BC的长,则B1C即可求得,根据正切的定义即可求解;
(3)按照(1)(2)的规律,画出含有7.5°角、15°角和30°角的直角三角形,如答图3所示,利用勾股定理、等腰三角形的性质及正切的定义,求出tan7.5°的值.
解答:解:(1)在Rt△ABC中,tan∠ABC=
,
则BC=
=
AC,
同理,B1C=
,
∵B1B=B1C-BC,
∴
-
AC=30,
解得:AC≈39(米);
(2)∵B1B=AB,
∴∠B1=∠B1AB=
∠ABC=15°,
设B1B=AB=x,
在Rt△ABC中,∠ABC=30°,
∴AC=
AB=
x,BC=
x,
∴B1C=x+
x,
∴tan15°=
=
=
=2-
;
(3)如答图3所示,图中三角形依次是含有7.5°角、15°角和30°角的直角三角形.
设AC=a,则AB=2a,BC=
=
a.
∴B1B=AB=2a,
∴B1C=2a+
a=(2+
)a.
在Rt△AB1C中,由勾股定理得:AB1=
=
=2
a,
∴B2B1=AB1=2
a,
∴B2C=B2B1+B1C=2
a+(2+
)a
∴tan7.5°=tan∠AB2C=
=
∴tan7.5°=
.

| AC |
| BC |
则BC=
| AC |
| tan30° |
| 3 |
同理,B1C=
| AC |
| tan22° |
∵B1B=B1C-BC,
∴
| AC |
| 0.40 |
| 3 |
解得:AC≈39(米);
(2)∵B1B=AB,
∴∠B1=∠B1AB=
| 1 |
| 2 |
设B1B=AB=x,
在Rt△ABC中,∠ABC=30°,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴B1C=x+
| ||
| 2 |
∴tan15°=
| AC |
| B1C |
| ||||
x+
|
| 1 | ||
2+
|
| 3 |
(3)如答图3所示,图中三角形依次是含有7.5°角、15°角和30°角的直角三角形.
设AC=a,则AB=2a,BC=
| AC |
| tan30° |
| 3 |
∴B1B=AB=2a,
∴B1C=2a+
| 3 |
| 3 |
在Rt△AB1C中,由勾股定理得:AB1=
| B1C2+AC2 |
(2+
|
2+
|
∴B2B1=AB1=2
2+
|
∴B2C=B2B1+B1C=2
2+
|
| 3 |
∴tan7.5°=tan∠AB2C=
| AC |
| B2C |
| a | ||||||
2
|
∴tan7.5°=
| 1 | ||||||
2
|

点评:此题考查了三角函数的基本概念,主要是正切概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO-OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).