题目内容
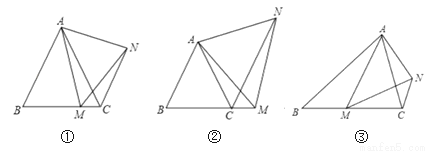
(1)如图①,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ACN=∠ABC.
【类比探究】
(2)如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ACN=∠ABC还成立吗?请说明理由.
【拓展延伸】
(3)如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
练习册系列答案
相关题目


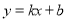 过点(-2,5),和直线
过点(-2,5),和直线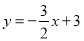 ,分别在下列条件下求这个一次函数的解析式.
,分别在下列条件下求这个一次函数的解析式.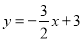 平行;
平行;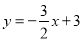 与y轴的交点关于
与y轴的交点关于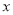 轴对称.
轴对称.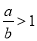 ,则
,则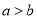 ; ②若
; ②若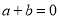 ,则
,则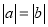 ;
;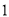 个 B.
个 B. 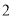 个 C.
个 C. 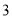 个 D.
个 D. 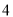 个
个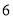 ,
, 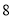 ,则第三边的平方是__________.
,则第三边的平方是__________.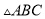 中,
中, 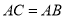 .两腰高线交于一点
.两腰高线交于一点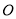 ,则描述
,则描述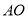 与
与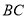 的关系最准确的是( ).
的关系最准确的是( ).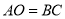 B.
B. 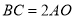 C. 垂直 D.
C. 垂直 D. 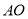 垂直平分
垂直平分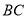
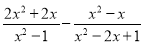 )÷
)÷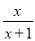 ,并解答:当
,并解答:当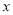 =1+
=1+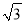 时,求原代数式的值.
时,求原代数式的值.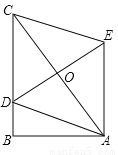
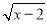 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )