题目内容
当k为何值时,关于x的方程(2-k)x2-2kx+1=0有两个相等的实数根?求出此时方程的根.
考点:根的判别式,一元二次方程的定义
专题:
分析:根据方程有两个相等的实数根,可得2-k≠0且△=b2-4ac=(-2k)2-4×(2-k)×1=4(k2+k-2)=0,解方程可得k的值,再把k的值代入方程(2-k)x2-2kx+1=0,解一元二次方程即可.
解答:解:∵关于x的方程(2-k)x2-2kx+1=0有两个相等的实数根,
∴2-k≠0且△=b2-4ac=(-2k)2-4×(2-k)×1=4(k2+k-2)=0,
解得:k=-2或1,
∴方程变为:4x2+4x+1=0,或x2-2x+1=0,
解得x1=x2=-
,或x1=x2=1.
∴2-k≠0且△=b2-4ac=(-2k)2-4×(2-k)×1=4(k2+k-2)=0,
解得:k=-2或1,
∴方程变为:4x2+4x+1=0,或x2-2x+1=0,
解得x1=x2=-
| 1 |
| 2 |
点评:此题主要考查了一元二次方程根的情况与判别式△的关系,以及一元二次方程的解法,关键是掌握:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知不等式组
无解,则a的取值范围是( )
|
| A、a>1 | B、a<1 |
| C、a≤1 | D、a≥1 |
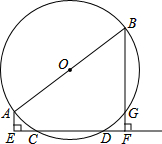 如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,BF交⊙O于G,下面的结论:(1)EC=DF;(2)AE+BF=AB;(3)AE=GF;(4)FG•FB=EC•ED;其中正确的结论是
如图,AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F,BF交⊙O于G,下面的结论:(1)EC=DF;(2)AE+BF=AB;(3)AE=GF;(4)FG•FB=EC•ED;其中正确的结论是 如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.
如图,AC=DB,∠ACB=∠DBC.找出图中所有的全等三角形,并说明理由.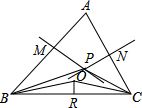 在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.
在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.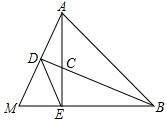 如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.
如图所示,AE、BD是△ABM的高,AE、BD交于点C,且AE=BE,BD平分∠ABM.