题目内容
为了适应我国经济发展的需要,我国铁路多数安装电力线路,并同时进行火车提速,已知A、B两地铁路长1200km,且从A地到B地火车每小时比原来多行驶20km,时间也比原来少用2h.
(1)求火车原来的速度.
(2)如果铁路在现有条件下安全行驶速度不得超过160km/h,问:现有条件下能否再次提速?若能,请说明还可以提多少;若不能,请说明理由.
(1)求火车原来的速度.
(2)如果铁路在现有条件下安全行驶速度不得超过160km/h,问:现有条件下能否再次提速?若能,请说明还可以提多少;若不能,请说明理由.
考点:分式方程的应用
专题:
分析:(1)设火车原来的速度为xkm/h,提速前后路程没变,关键描述语为:“从A地到B地火车每小时比原来多行驶20km,时间也比原来少用2h”;等量关系为:提速前的列车所用时间=提速后的列车所用时间+2;
(2)将(1)中所求x的值加上20,所得结果与160进行比较,进而求解即可.
(2)将(1)中所求x的值加上20,所得结果与160进行比较,进而求解即可.
解答:解:(1)设火车原来的速度为xkm/h.
则:
=
+2,
解得:x1=100,x2=-120(舍去),
经检验x=100是原方程的根.
答:火车原来的速度是100km/h;
(2)由(1)知x+20=120<160,
所以现有条件下能再次提速,还可以提速160-120=40(km/h).
则:
| 1200 |
| x |
| 1200 |
| x+20 |
解得:x1=100,x2=-120(舍去),
经检验x=100是原方程的根.
答:火车原来的速度是100km/h;
(2)由(1)知x+20=120<160,
所以现有条件下能再次提速,还可以提速160-120=40(km/h).
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
 C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE.
C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE.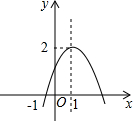 如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论:
如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(-1,0),顶点为(1,2),则结论: 某轮船由西向东航行,在A处测得小岛P的方位是北偏东70°,又继续航行7海里后,在B处测得小岛P的方位是北偏东50°,则此时轮船与小岛P的距离BP=
某轮船由西向东航行,在A处测得小岛P的方位是北偏东70°,又继续航行7海里后,在B处测得小岛P的方位是北偏东50°,则此时轮船与小岛P的距离BP=