题目内容
6．
如图，△ABC中，∠A=36°，D是AC上一点，且AD=DB=BC，求证：AB=AC．
分析 根据等腰三角形的性质得到∠ABD=∠A=36°，由外角的性质得到∠BDC=∠A+∠ABD=72°，由DB=BC，得到∠C=∠BDC=72°，根据三角形的内角和得到∠ABC=180°-∠A-∠C=72°，即可得到结论．
解答 解：∵AD=DB，
∴∠ABD=∠A=36°，
∴∠BDC=∠A+∠ABD=72°，
∵DB=BC，
∴∠C=∠BDC=72°，
∴∠ABC=180°-∠A-∠C=72°，
∴∠ABC=∠C，
∴AB=AC．
点评 本题主要考查等腰三角形的性质和判定，三角形的外角的性质，三角形的内角和，掌握等角对等边是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图．已知△ABC为等边三角形，D、E分别是AB、AC上的点．且BD=CE，AE、CD相交于F．试求∠AFD的度数．
如图，已知AB和CD是⊙0的两条弦，$\widehat{AC}=\widehat{BD}$，求证：AB=CD．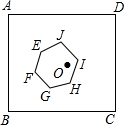
如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为$\frac{\sqrt{2}-1}{2}$．