题目内容
17. 如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )| A. | ∠BAD=∠EDC | B. | ∠BAD=2∠EDC | C. | ∠BAD+∠EDC=45° | D. | ∠BAD+∠EDC=60° |
分析 根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠EDC.
解答 解:∠BAD=2∠CDE.理由如下:
∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠EDC,
即∠BAD=2∠EDC.
故选:B.
点评 本题主要考查学生运用等腰三角形性质,三角形的外角性质进行推理的能力,题目比较典型,是一道很好的题目,关键是进行推理和总结规律.

练习册系列答案
相关题目
5.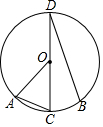 如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )
如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )
 如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )
如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )| A. | 25° | B. | 45° | C. | 50° | D. | 60° |
12.从-2,-1,-$\frac{1}{2}$,1,2这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组$\left\{\begin{array}{l}{2x+7≥9}\\{x-a<0}\end{array}\right.$无解,且使分式方程$\frac{a}{2x-3}$+$\frac{a-2}{2x-3}$=-1的解为正分数,那么这五个数中所有满足条件的a的值之和是( )
| A. | -3 | B. | -$\frac{5}{2}$ | C. | -2 | D. | -$\frac{7}{2}$ |
2. 如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )
如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )
 如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )
如图,在△ABC中,点P在边AB上,则在下列四个条件中::①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
9.下列说法中正确的有( )
①过一点有且只有一条直线与已知直线垂直;
②如果两个角相等,那么这两个角是对顶角;
③如果两条直线被第三条直线所截,那么内错角相等;
④联结直线外一点与直线上各点的所有线段,垂线段最短;
⑤邻补角的平分线互相垂直.
①过一点有且只有一条直线与已知直线垂直;
②如果两个角相等,那么这两个角是对顶角;
③如果两条直线被第三条直线所截,那么内错角相等;
④联结直线外一点与直线上各点的所有线段,垂线段最短;
⑤邻补角的平分线互相垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列长度的三条线段能组成三角形的是( )
| A. | 1cm 2cm 3cm | B. | 1cm 2cm 3.5cm | C. | 5cm 8cm 12cm | D. | 4cm 5cm 9cm |
7.禽流感病毒的形状一般为球形,直径大约为0.000000102m,该直径用科学记数法表示为( )
| A. | 102×10-7m | B. | 1.02×10-7m | C. | 102×10-6m | D. | 1.02×10-8m |