题目内容
 如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是
如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是考点:平面展开-最短路径问题
专题:
分析:由于圆锥的底面周长也就是圆锥的侧面展开图的弧长,利用弧长公式即可求得侧面展开图的圆心角,进而构造直角三角形求得相应线段即可.
解答: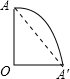 解:圆锥的侧面展开图,如图所示:
解:圆锥的侧面展开图,如图所示:
∵圆锥的底面周长=2π×5=10π,
设侧面展开图的圆心角的度数为n.
∴
=10π,
解得n=90,
∴最短路程为:
=20
.
故答案为:20
.
 解:圆锥的侧面展开图,如图所示:
解:圆锥的侧面展开图,如图所示:∵圆锥的底面周长=2π×5=10π,
设侧面展开图的圆心角的度数为n.
∴
| nπ×20 |
| 180 |
解得n=90,
∴最短路程为:
| 202+202 |
| 2 |
故答案为:20
| 2 |
点评:本题考查的是平面展开-最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
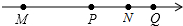 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
下列事件属必然事件的是( )
| A、打开电视,正在直播NBA篮球赛 |
| B、早晨太阳一定从东方升起 |
| C、掷两次硬币,一定有一次正面朝上 |
| D、365人中一定有两人同一天出生 |
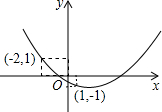 如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,-1)和(-2,1),下列关于此二次函数的叙述,正确的是( )| A、当x=0时,y的值小于-1 |
| B、当x=-3时,y的值大于1 |
| C、当x=5时,y的值等于0 |
| D、当x=1时,y的值大于1 |
 如图,是由4个大小相同的正方体搭成的几何体,其主视图是( )
如图,是由4个大小相同的正方体搭成的几何体,其主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4 为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为
为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为 如图,点A、B、C、D在⊙O上,AC、BD交于点E,若CD:AB=1:2,△ABE的周长为8,则△CDE的周长为
如图,点A、B、C、D在⊙O上,AC、BD交于点E,若CD:AB=1:2,△ABE的周长为8,则△CDE的周长为