题目内容
 在如图的4×3网格中,每个小正方形的边长均为1,正方形顶点叫网格格点,连结两个网格格点的线段叫网格线段.
在如图的4×3网格中,每个小正方形的边长均为1,正方形顶点叫网格格点,连结两个网格格点的线段叫网格线段.(1)请你画一个边长为
| 5 |
(2)若a是图中能用网格线段表示的最大无理数,b是图中能用网格线段表示的最小无理数,求a2-2b2的平方根.
考点:作图—复杂作图,平方根,勾股定理,菱形的性质
专题:
分析:(1)直接利用勾股定理以及菱形的性质得出符合题意的图形求出其面积;
(2)利用网格直接得出最大的无理数以及最小的无理数,再利用平方根的定义得出即可.
(2)利用网格直接得出最大的无理数以及最小的无理数,再利用平方根的定义得出即可.
解答: 解:(1)如图所示:四边形ABCD是边长为
解:(1)如图所示:四边形ABCD是边长为
的菱形,
其面积为:
BD×AC=
×2×4=4;
(2)由网格得出:
用网格线段表示的最大无理数为:
=2
,
图中能用网格线段表示的最小无理数为:
,
∴a2-2b2=(2
)2-2×(
)2=16,
∴a2-2b2的平方根是:±4.
 解:(1)如图所示:四边形ABCD是边长为
解:(1)如图所示:四边形ABCD是边长为| 5 |
其面积为:
| 1 |
| 2 |
| 1 |
| 2 |
(2)由网格得出:
用网格线段表示的最大无理数为:
| 42+22 |
| 5 |
图中能用网格线段表示的最小无理数为:
| 2 |
∴a2-2b2=(2
| 5 |
| 2 |
∴a2-2b2的平方根是:±4.
点评:此题主要考查了菱形的判定与性质以及平方根的定义等知识,正确把握菱形的性质是解题关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列图形中,既是中心对称图形,又是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在0.1,-3,
和
这四个实数中,无理数是( )
| 2 |
| 1 |
| 3 |
| A、0.1 | ||
| B、-3 | ||
C、
| ||
D、
|
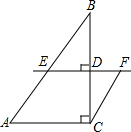 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DE于F.设CD=x.