题目内容
7.某商店销售一种台灯,若按每个12元的价格销售,每周可卖出50个,若按每个15元的价格销售,每周可卖出35个,已知每周销售量y(个)与价格x(元/个)之间满足一次函数关系.(1)试求y与x之间的函数关系式;
(2)这种台灯的进价是10元/个,当价格定位多少时,才能使每周的销售利润最大?最大利润是多少?
分析 (1)设y与x之间的函数关系式为y=kx+b,通过已知的数据建立方程组求出其解即可;
(2)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
解答 解:(1)设y与x之间的函数关系式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{50=12k+b}\\{35=15k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=110}\end{array}\right.$.
故y与x的函数关系式为:y=-5x+110;
(2)∵y=-5x+110,
∴W=(x-10)y=(x-10)(-5x+110)
=-5x2+160x-1100
=-5(x-16)2+180,
∵a=-5<0,
∴当x=16时,W最大=180,
∴售价定为16元/件时,每周的最大利润W=180元.
点评 本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
17.不等式组$\left\{\begin{array}{l}{x-1>0}\\{2x+3>x}\end{array}\right.$的解集是( )
| A. | x>1 | B. | x>-3 | C. | -3<x<1 | D. | -1<x<3 |
18.下列命题中真命题是( )
| A. | 位似图形一定是相似形 | B. | 相似形一定是位似图形 | ||
| C. | 两个直角三角形是相似三角形 | D. | 两个直角三角形是位似三角形 |
15.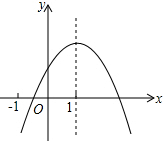 如图,二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线,下列式子成立的是( )
如图,二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线,下列式子成立的是( )
 如图,二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线,下列式子成立的是( )
如图,二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线,下列式子成立的是( )| A. | abc>0 | B. | b<a+c | C. | a+b+c<0 | D. | 2c<3b |
2.去年区教育局开展了认领“文明清单”活动,今年开学为落实认领“文明清单”活动,我校初一、初二两个年组对活动情况进行了统计,落实后的清单条数由落实前的清单条数与落实后认领的条数两部分组成(已知落实前每个年组的清单条数相同,落实后人均条数一样),如表是初一、初二的学生数及落实后清单条数的情况信息.
(1)试求落实前各年组的清单总数及落实后人均认领清单条数?
(2)如果初三年级想要清单条数超过2480条,那么初三年级组人均至少应该认领多少条?
| 初一 | 初二 | 初三 | |
| 人数 | 200 | 180 | 210 |
| 清单总数(条) | 1800 | 1700 |
(2)如果初三年级想要清单条数超过2480条,那么初三年级组人均至少应该认领多少条?
 如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.
如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.