题目内容
6.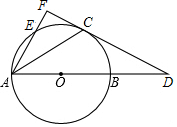 如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.
如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.(1)求证:DC是⊙O的切线;
(2)若⊙O的半径为3,sinD=$\frac{3}{5}$,求线段AF的长.
分析 (1)连接OC,由AB是⊙O的直径,得到∠ACB=90°,即∠1+∠3=90°.根据等腰三角形的性质得到∠1=∠2.得到∠DCB+∠3=90°.于是得到结论;
(2)根据三角函数的定义得到OD=5,AD=8.根据圆周角定理得到∠2=∠4.推出OC∥AF.根据相似三角形的性质即可得到结论.
解答 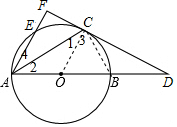 (1)证明:连接OC,BC,
(1)证明:连接OC,BC,
∵AB是⊙O的直径,
∴∠ACB=90°,即∠1+∠3=90°.
∵OA=OC,
∴∠1=∠2.
∵∠DCB=∠BAC=∠1.
∴∠DCB+∠3=90°.
∴OC⊥DF.
∴DF是⊙O的切线;
(2)解:在Rt△OCD中,OC=3,sinD=$\frac{3}{5}$.
∴OD=5,AD=8.
∵$\widehat{CE}$=$\widehat{BC}$,
∴∠2=∠4.
∴∠1=∠4.
∴OC∥AF.
∴△DOC∽△DAF.
∴$\frac{OC}{AF}=\frac{OD}{AD}$.
∴AF=$\frac{24}{5}$.
点评 本题考查了切线的判定,圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.某校有两种类型的学生宿舍30间,大宿舍每间可住8人,小宿舍每间可住5人.该校198个住宿生恰好住满30间宿舍.设大宿舍有x间,小宿舍有y间,得方程组( )
| A. | $\left\{\begin{array}{l}5x+8y=198\\ x+y=30\end{array}\right.$ | B. | $\left\{\begin{array}{l}8x+5y=198\\ x+y=30\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=198\\ 8x+5y=30\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=198\\ 5x+8y=30\end{array}\right.$ |
1. 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )
 如图,阴影部分是一个长方形,它的面积是( )
如图,阴影部分是一个长方形,它的面积是( )| A. | 3cm2 | B. | 4cm2 | C. | 5cm2 | D. | 6cm2 |
15.已知圆锥的底面半径为2cm,母线长为3cm,则它的侧面展开图的面积为( )
| A. | 18πcm2 | B. | 12πcm2 | C. | 6πcm2 | D. | 3πcm2 |
 正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$.
正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )