题目内容
10.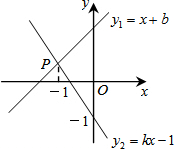 如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )| A. |  | B. | 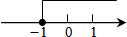 | C. | 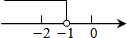 | D. | 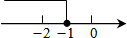 |
分析 观察函数图象得到当x≤-1时,函数y1=x+b的图象都在y2=kx-1的图象下方,所以不等式x+b≤kx-1的解集为x≤-1,然后根据用数轴表示不等式解集的方法对各选项进行判断.
解答 解:根据题意得当x≤-1时,y1≤y2,
所以不等式x+b≤kx-1的解集为x≤-1.
故选D.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了在数轴上表示不等式的解集.

练习册系列答案
相关题目
20.下列说法中,正确的是( )
| A. | 0是最小的整数 | B. | 最大的负整数是-1 | ||
| C. | 任何有理数的绝对值都是正数 | D. | 一个有理数的平方总是正数 |
1.随意掷两个均匀的骰子,朝上面的点数之和是10的概率是( )
| A. | $\frac{1}{12}$ | B. | 1 | C. | $\frac{1}{18}$ | D. | 0 |
15.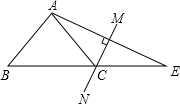 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 60° | C. | 50° | D. | 55° |
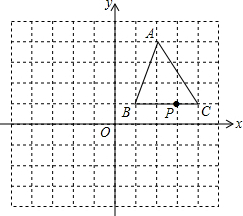 如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.
如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.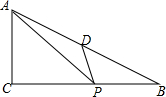 如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.
如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.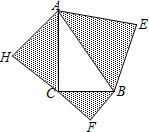 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.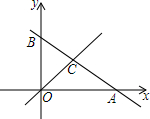 如图,直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B,直线y2过原点O且与直线
如图,直线y1=-$\frac{1}{2}$x+2与x轴、y轴分别交于点A和点B,直线y2过原点O且与直线