题目内容
12.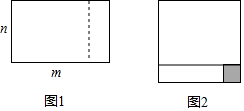 如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )
如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )| A. | 图2所示的长方形是正方形 | |
| B. | 图2所示的长方形周长=2m+2n | |
| C. | 阴影部分所表示的小正方形边长=m-n | |
| D. | 阴影部分所表示的小正方形面积=$\frac{(m-n)^{2}}{4}$ |
分析 设小正方形的边长为a,C、根据图形的拼法可得出关于a的一元一次方程,解之即可用含m、n的代数式表示出a的值,由此得出C选项不符合题意;A、观察图形2找出图形2中长方形的相邻两边长,由此可得出该长方形为正方形,即A选项符合题意;B、根据正方形的周长公式即可找出图形2的周长,再代入a值即可得知B选项符合题意;D、根据正方形的面积公式,再代入a值,即可得知D选项符合题意.综上即可得出结论.
解答 解:设小正方形的边长为a,
C、根据图形的拼法可知:m-a=n+a,
∴a=$\frac{m-n}{2}$,
∴C选项不符合题意;
A、∵图2中长方形相邻两边长度分别为n+a,n+a,
∴图2所示的长方形是正方形,
∴A选项符合题意;
B、∵图2所示的长方形周长=4(n+a)=4(n+$\frac{m-n}{2}$)=4×$\frac{m+n}{2}$=2m+2n,
∴B选项符合题意;
D、∵阴影部分所表示的小正方形面积=a2=$(\frac{m-n}{2})^{2}$=$\frac{(m-n)^{2}}{4}$,
∴D选项符合题意.
故选C.
点评 本题考查了完全平方公式的几何背景、正方形的周长及面积,根据图形的拼法找出小正方形的边长,再逐一分析四个选项的正误是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
14.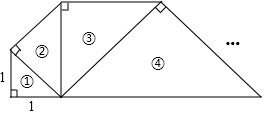 如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为( )
如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为( )
 如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为( )
如图,一系列等腰直角三角形(编号分别为①、②、③、④、…)组成了一个螺旋形,其中第1个三角形的直角边长为1,则第n个等腰直角三角形的面积为( )| A. | 2n-3 | B. | 2n-2 | C. | 2n-1 | D. | 2n |
12.去年我县12月份某天的最低气温为-6℃,最高气温为-2℃,那么这一天的最高气温比最低气温高( )
| A. | 4℃ | B. | -4℃ | C. | 8℃ | D. | -8℃ |
7.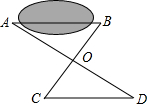 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
 要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )
要测量池塘的宽度AB,画出如图所示的两个三角形,下面测出的哪组条件不能使CD=AB( )| A. | OA=OD,OB=OC | B. | ∠B=∠C,OB=OC | C. | ∠B=∠C,OA=OD | D. | ∠C=∠B,∠A=∠D |
17.一个水池有甲、乙两个水龙头,单独开甲水龙头2小时可把空池灌满;单独开乙水龙头3小时可把空池灌满,若同时开放两个水龙头,灌满水池需( )
| A. | $\frac{6}{5}$小时 | B. | $\frac{5}{6}$小时 | C. | 2小时 | D. | 3小时 |
4. 已知:如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠A=30°,则线段AB与BD的数量关系是( )
已知:如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠A=30°,则线段AB与BD的数量关系是( )
 已知:如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠A=30°,则线段AB与BD的数量关系是( )
已知:如图,在△ABC中,∠ACB=90°,CD是边AB上的高,∠A=30°,则线段AB与BD的数量关系是( )| A. | AB=2BD | B. | AB=3BD | C. | AB=4BD | D. | AB=5BD |