题目内容
11.已知抛物线与x轴交于A(6,0)、B(-$\frac{5}{4}$,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.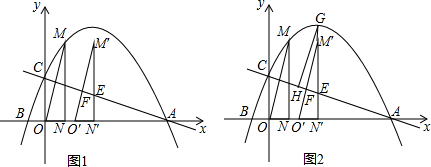
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,M′N′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
分析 (1)设抛物线解析式为y=a(x-6)(x+$\frac{5}{4}$),把点M(1,3)代入即可求出a,进而解决问题.
(2))①如图1中,AC与OM交于点G.连接EO′,首先证明△AOC∽△MNO,推出OM⊥AC,在RT△EO′M′中,利用勾股定理列出方程即可解决问题.
②由△GHE∽△AOC得$\frac{EG}{HE}$=$\frac{AC}{CO}$=$\sqrt{19}$,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
解答 解:(1)设抛物线解析式为y=a(x-6)(x+$\frac{5}{4}$),把点M(1,3)代入得a=-$\frac{4}{15}$,
∴抛物线解析式为y=-$\frac{4}{15}$(x-6)(x+$\frac{5}{4}$),
∴y=-$\frac{4}{15}$x2+$\frac{19}{15}$x+2.
(2)①如图1中,AC与OM交于点G.连接EO′.
∵AO=6,OC=2,MN=3,ON=1,
∴$\frac{AO}{OC}$=$\frac{MN}{ON}$=3,
∴$\frac{AO}{MN}$=$\frac{OC}{ON}$,∵∠AOC=∠MON=90°,
∴△AOC∽△MNO,
∴∠OAC=∠NMO,
∵∠NMO+∠MON=90°,
∴∠MON+∠OAC=90°,
∴∠AGO=90°,
∴OM⊥AC,
∵△M′N′O′是由△MNO平移所得,
∴O′M′∥OM,
∴O′M′⊥AC,
∵M′F=FO′,
∴EM′=EO′,
∵EN′∥CO,
∴$\frac{EN′}{CO}$=$\frac{AN′}{AO}$,
∴$\frac{EN′}{2}$=$\frac{5-t}{6}$,
∴EN′=$\frac{1}{3}$(5-t),
在RT△EO′N′中,∵O′N′=1,EN′=$\frac{1}{3}$(5-t),EO′=EM′=$\frac{4}{3}$+$\frac{1}{3}$t,
∴($\frac{4}{3}$+$\frac{1}{3}$t)2=1+($\frac{5}{3}$-$\frac{1}{3}$t)2,
∴t=1.
②如图2中,
∵GH∥O′M′,O′M′⊥AC,
∴GH⊥AC,
∴∠GHE=90°,
∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,
∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,
∴△GHE∽△AOC,
∵AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$
∴$\frac{EG}{HE}$=$\frac{AC}{CO}$=$\frac{2\sqrt{10}}{2}$=$\sqrt{10}$,
∴EG最大时,EH最大,
∵EG=GN′-EN′=-$\frac{4}{15}$(t+1)2+$\frac{19}{15}$(t+1)+2-$\frac{1}{3}$(5-t)=-$\frac{4}{15}$t2+$\frac{16}{15}$t+$\frac{4}{3}$=-$\frac{4}{15}$(t-2)2+$\frac{12}{5}$.
∴t=2时,EG最大值=$\frac{12}{5}$,
∴EH最大值=$\frac{6\sqrt{10}}{25}$.
∴t=2时,EH最大值为$\frac{6\sqrt{10}}{25}$.
点评 本题考查二次函数综合题、相似三角形的判定和性质、勾股定理等知识,解题的关键是发现OM⊥CA,学会利用转化的思想解决问题,学会构建二次函数解决最值问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | a-c>b-c | B. | c-a>c-b | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )| A. | 61° | B. | 51° | C. | 50° | D. | 60° |
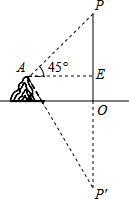 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )| A. | $25\sqrt{3}+75$ | B. | $50\sqrt{3}+50$ | C. | $75\sqrt{3}+75$ | D. | $50\sqrt{3}+100$ |
| A. | 0.245×104 | B. | 2.45×103 | C. | 24.5×102 | D. | 2.45×1011 |
 如图,在菱形ABCD中,对角线AC、BD相交于点O,若AC=6,BD=8,则菱形ABCD的周长是20.
如图,在菱形ABCD中,对角线AC、BD相交于点O,若AC=6,BD=8,则菱形ABCD的周长是20.