题目内容
15.已知关于x的一元二次方程x2+$\sqrt{15}$x+2m-1=0.(1)请你为m选取一个合适的正整数,使得到的方程有两个不相等的实数根;
(2)设x1,x2是(1)中所得到的方程的两个实数根,求x12+x22+x1x2的值.
分析 (1)根据△>0求得m的取值范围,再进一步在范围之内确定m的一个整数值;
(2)根据根与系数的关系,对x12+x22+x1x2进行变形求解.
解答 解:(1)∵方程有两个不相等的实数根,
∴△=b2-4ac=15-4(2m-1)>0,解得m<$\frac{19}{8}$.
∴m=1.
(2)当m=1时,则得方程x2+$\sqrt{15}$x+1=0,
∵x1,x2是方程x2+4x=0的两个实数根,
∴x1+x2=-$\sqrt{15}$,x1x2=1,
∴x12+x22+x1x2=(x1+x2)2-x1x2=(-$\sqrt{15}$)2-1=14.
点评 此题考查一元二次方程根的情况与判别式△的关系:①△>0?方程有两个不相等的实数根;②△=0?方程有两个相等的实数根;③△<0?方程没有实数根.以及根与系数的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.抛物线的解析式y=-2(x+3)2+1,则顶点坐标是( )
| A. | (-3,1) | B. | (3,1) | C. | (3,-1) | D. | (1,3) |
20.下表是某商品的数量x(个)与售价y(元)的对应关系,根据表中提供的信息可知y与x之间的关系式是y=8x.
| 数量x(个) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 8 | 16 | 24 | 32 | 40 |
5.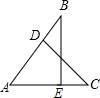 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
 如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )
如图,AB=AC,∠AEB=∠ADC=90°,则判断△ABE≌△ACD的方法是( )| A. | AAS | B. | HL | C. | SSS | D. | SAS |
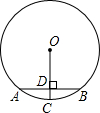 如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.
如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.