题目内容
6.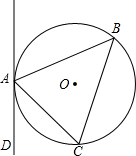 如图,△ABC是⊙O的内接三角形,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
如图,△ABC是⊙O的内接三角形,∠CAD=∠ABC,判断直线AD与⊙O的位置关系,并说明理由.
分析 连接AO,并延长交⊙O于E,连接CE,由圆周角定理可知∠E=∠ABC,∠ACE=90°,进而根据∠CAD=∠ABC能求出∠EAD=90°,
解答  解:直线AD是⊙O的切线;
解:直线AD是⊙O的切线;
理由:连接AO,并延长交⊙O于E,连接CE,
∵∠CAD=∠ABC,∠E=∠ABC,
∴∠E=∠CAD,
∵AE是直径,
∴∠ACE=90°,
∴∠E+∠CAE=90°,
∴∠CAE+∠CAD=90°,
即EA⊥AD,
∴直线AD与⊙O相切.
点评 本题考查了切线的判定,解直角三角形等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.下列说法①任意一个数都有两个平方根;②任意一个数都有立方根;③-125的立方根是±5;④$\frac{\sqrt{3}}{2}$是一个分数;⑤两个无理数的积是一个有理数;⑥但0<a<1时,$\root{3}{a}$$>\sqrt{a}$,其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.已知一个三角形的周长为18cm,且它的角平分线的交点到一边的距离是2.5cm,则这个三角形的面积是( )
| A. | 22.5cm2 | B. | 19cm2 | C. | 21cm2 | D. | 23.5cm2 |
1.将函数y=-x2的图象如何平移得到y=-x2-8x-7的图象( )
| A. | 向左平移4个单位,再向上平移9个单位 | |
| B. | 向左平移4个单位,再向下平移9单位 | |
| C. | 向右平移4个单位,再向上平移9单位 | |
| D. | 向右平移4个单位,再向下平移9单位 |
16.下列说法正确的是( )
| A. | 2,3,$\sqrt{13}$是一组勾股数 | |
| B. | 估算得$\sqrt{5}$$<\root{3}{7}$ | |
| C. | 无理数是无限小数 | |
| D. | 在海面上知道一个方位角就可以确定一个目标的位置 |
 如图是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形,这样的白色小方格有( )
如图是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在要从其余13个白色小方格中选出一个也涂成黑色的图形称为轴对称图形,这样的白色小方格有( ) 如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
如图,∠A=90°,E为BC上的一点,A点和E点关于BD的对称,B点、C点关于DE对称,求∠ABC和∠C的度数.