题目内容
4. 现有一张矩形纸片ABCD,要将点D沿某条直线EF翻折180°,恰好落在BC边上的点D′处,直线EF与AD交于点E,与BC交于点F.
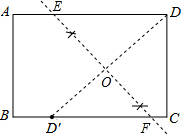
现有一张矩形纸片ABCD,要将点D沿某条直线EF翻折180°,恰好落在BC边上的点D′处,直线EF与AD交于点E,与BC交于点F.(1)请利用尺规作图在图中作出该直线EF;(保留作图痕迹,不写作法)
(2)在(1)的条件下,在矩形ABCD中,若AD=10,AB=6,BD′=2,请计算纸片ABCD折叠后产生的折痕EF的长度.
分析 (1)连接DD′,作DD′的垂直平分线即可解决问题;
(2)在Rt△DD′C中,利用勾股定理求出DD′,再根据tan∠EDO=tan∠DD′C,可得$\frac{EO}{OD}$=$\frac{DC}{CD′}$,由此即可求出OE,只要证明OF=OE即可解决问题;
解答 解:(1)如图,直线EF即为所求.
.
(2)设EF交DD′于O.
在Rt△DCD′中,∵∠DCD′=90°,DC=AB=6,CD′=BC-BD′=8,
∴DD′=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴OD=OD′=5,
∵AD∥BC,
∴∠EDO=∠DD′C,
∴tan∠EDO=tan∠DD′C,
∴$\frac{EO}{OD}$=$\frac{DC}{CD′}$,
∴$\frac{EO}{5}$=$\frac{8}{6}$,
∴EO=$\frac{20}{3}$,
∵$\frac{EO}{OF}$=$\frac{OD}{OD′}$=1,
∴OF=OE=$\frac{20}{3}$,
∴EF=$\frac{40}{3}$.
点评 本题考查轴对称变换、矩形的性质、锐角三角函数、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.一元一次方程$\frac{x}{1×3}$+$\frac{x}{3×5}$+$\frac{x}{5×7}$+…+$\frac{x}{2013×2015}$=$\frac{2014}{2015}$的解是( )
| A. | 1 | B. | 2 | C. | 2014 | D. | 2015 |
19.若多项式x2+px+12可以因式分解为(x+m)(x+n)的形式,且p、m、n均为整数,则满足条件的整数p共有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
16.已知关于x的一元二次方程2x2-3kx+4的一个根是1,则k等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 1 |
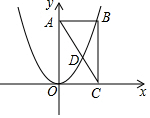 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$. 如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)
如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)