题目内容
19.解方程:4x2-12x-2=3.分析 首先把方程化成一般形式,求出b2-4ac的值,然后代入求根公式进行计算即可.
解答 解:4x2-12x-2=3,
整理得:4x2-12x-5=0.
∵a=4,b=-12,c=-5,
∴b2-4ac=(-12)2-4×4×(-5)=224>0,
∴x=$\frac{12±\sqrt{224}}{2×4}$=$\frac{12±4\sqrt{14}}{8}$=$\frac{3±\sqrt{14}}{2}$,
∴x1=$\frac{3+\sqrt{14}}{2}$,x2=$\frac{3-\sqrt{14}}{2}$.
点评 本题主要考查了一元二次方程的解法--公式法;熟练掌握求根公式,正确求出判别式的值是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.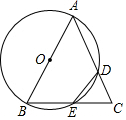 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
 如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )
如图,在△ABC中,AB=AC,以AB为直径的圆分别交边AC,BC于点D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,则∠DEC的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
11.(1)$\frac{sin30°}{sin60°-cos45°}$-tan60°-tan45°
(2)cos30°-|sin60°-tan45°|+(2sin45°+1)0-(sin30°)-2.
(2)cos30°-|sin60°-tan45°|+(2sin45°+1)0-(sin30°)-2.
9.在下列代数式中,次数为3的单项式是( )
| A. | x2y | B. | xy3 | C. | x3+y3 | D. | 3xy |