题目内容
14.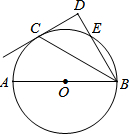 如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.(1)求证:BC平分∠DBA;
(2)连接AE和AC,若cos∠ABD=$\frac{1}{2}$,OA=m,请写出求四边形AEDC面积的思路.
分析 (1)如图1中,连接OC,由CD是⊙O的切线,推出OC⊥CD,由BD⊥CD,推出OC∥BD,推出∠OCB=∠CBD,由OC=OB,推出∠OCB=∠OBC,即可推出∠CBO=∠CBD;
(2)如图连接AC、AE.易知四边形AEDC是直角梯形,求出CD、AE、DE即可利用梯形面积公式计算即可.
解答 (1)证明:如图1中,连接OC,
∵CD是⊙O的切线,
∴OC⊥CD,∵BD⊥CD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBO=∠CBD,
∴BC平分∠DBA
(2)解:如图连接AC、AE.
∵cos∠ABD=$\frac{1}{2}$,
∴∠ABD=60°,
由(1)可知,∠ABC=∠CBD=30°,
在Rt△ACB中,∵∠ACB=90°,∠ABC=30°,AB=2m,
∴BC=AB•cos30°=$\sqrt{3}$m,
在Rt△ABE中,∵∠AEB=90°,∠BAE=30°,AB=2m,
∴BE=$\frac{1}{2}$AB=m,AE=$\sqrt{3}$m,
在Rt△CDB中,∵∠D=90°,∠CBD=30°,BC=$\sqrt{3}$m,
∴CD=$\frac{1}{2}$BC=$\frac{\sqrt{3}}{2}$m,BD=$\frac{3}{2}$m,
∴DE=DB-BE=$\frac{1}{2}$m.
∴S梯形AEDC=$\frac{1}{2}$•(CD+AE)•DE=$\frac{3\sqrt{3}}{8}$m2.
解题思路:写通顺即可!
点评 本题考查切线的性质、解直角三角形、角平分线的定义、解直角三角形等特殊角三角函数、等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
 已知:如图,∠A=∠D=90°,AC=BD
已知:如图,∠A=∠D=90°,AC=BD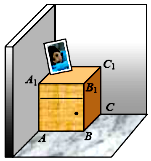 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
 如图,直线y=-x+m与y=nx+b(n≠0)的交点的横坐标为-2,有下列结论:①当x=-2时,两个函数的值相等;②b=4n;③关于x的不等式nx+b>0的解集为x>-4;④x>-2是关于x的不等式-x+m>nx+b的解集,其中正确结论的序号是①②③.(把所有正确结论的序号都填在横线上)
如图,直线y=-x+m与y=nx+b(n≠0)的交点的横坐标为-2,有下列结论:①当x=-2时,两个函数的值相等;②b=4n;③关于x的不等式nx+b>0的解集为x>-4;④x>-2是关于x的不等式-x+m>nx+b的解集,其中正确结论的序号是①②③.(把所有正确结论的序号都填在横线上)
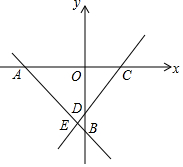 如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)
如图,直线AB交x轴,y轴于A(-3,0),B两点,直线CD交x轴,y轴于C,D(0,-2)两点,直线AB,CD相交于点E(-$\frac{1}{2}$,$-\frac{5}{2}$)