��Ŀ����
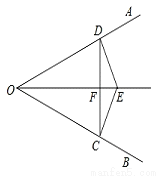
��ͼ����֪��E�ǡ�AOB��ƽ������һ�㣬EC��OB��ED��OA��C��D�Ǵ���.����CD���ҽ�OE�ڵ�F��
��1����֤��OE��CD�Ĵ�ֱƽ���ߣ�
��2������AOB=60�㣬��֤��OE=4EF��
��ϰ��ϵ�д�
 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����֪��E�ǡ�AOB��ƽ������һ�㣬EC��OB��ED��OA��C��D�Ǵ���.����CD���ҽ�OE�ڵ�F��
��1����֤��OE��CD�Ĵ�ֱƽ���ߣ�
��2������AOB=60�㣬��֤��OE=4EF��

 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�