题目内容
8.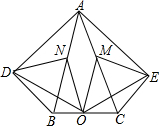 在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.(1)求证:△EMO≌△OND;
(2)若AB=AC,且∠BAC=40°,当∠DAB等于多少时,四边形ADOE是菱形,并证明.
分析 (1)根据直角三角形斜边中线等于斜边一半得:DN=$\frac{1}{2}$AB,由中位线定理得:OM=$\frac{1}{2}$AB,则OM=DN,同理得:ON=ME,再根据外角定理和已知证明其夹角相等,则两三角形全等;
(2)连接AO,当∠DAB等于35°时,四边形ADOE是菱形,如图2,设∠DAB=x°,则∠BND=2x°,易证得OD=OE,AD=AE,因此只要AD=OD,四边形ADOE就是菱形;即∠DAO=∠AOD,列关于x的方程解出即可.
解答 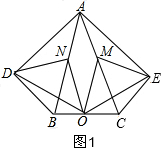 证明:(1)∵∠ADB=90°,N是AB的中点,
证明:(1)∵∠ADB=90°,N是AB的中点,
∴DN=$\frac{1}{2}$AB=AN,
∴∠ADN=∠BAD,
∵O是AB的中点,M是AC的中点,
∴OM是△ABC的中位线,
∴OM=$\frac{1}{2}$AB,OM∥AB,
∴∠OMC=∠BAC,
同理得:∠BNO=∠BAC,
∴∠BNO=∠OMC,
∵DN=$\frac{1}{2}$AB,OM=$\frac{1}{2}$AB,
∴DN=OM,
同理得:ME=ON,
∵∠BND=∠ADN+∠BAD,
∠CME=∠CAE+∠AEM,
∴∠BND=2∠BAD,∠CME=2∠CAE,
∵∠BAD=∠CAE,
∴∠BND=∠CME,
∴∠BND+∠BNO=∠CME+∠OMC,
即∠DNO=∠EMO,
∴△EMO≌△OND;
(2)当∠DAB等于35°时,四边形ADOE是菱形,理由是:
如图2,连接AO,
设∠DAB=x°,则∠BND=2x°,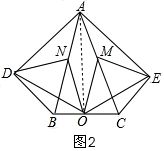
∵AB=AC,O是BC的中点,
∴AO平分∠BAC,AO⊥BC,
∵∠BAC=40°,
∴∠BAO=20°,
在Rt△ABO中,N是AB的中点,
∴ON=$\frac{1}{2}$AB=AN,
∴∠BAO=∠AON=20°,
∴∠BNO=40°,
由(1)得:ON=$\frac{1}{2}$AC,DN=$\frac{1}{2}$AB,
∴ON=DN,
∴∠NDO=∠NOD=$\frac{180-∠DNO}{2}$=90°-$\frac{1}{2}$(2x°+40°)=70°-x°,
∵∠ADB=∠AEC=90°,∠BAD=∠CAE,AB=AC,
∴△ADB≌△AEC,
∴AD=AE,
由(1)得:△EMO≌△OND,
∴OD=OE,
∴当AD=OD时,四边形ADOE是菱形,
即∠DAO=∠AOD,
x+20=70-x+20,
x=35,
∴当∠DAB等于35°时,四边形ADOE是菱形.
点评 本题考查了直角梯形的性质、菱形、全等三角形、等腰三角形性质等知识点的理解和掌握,综合运用性质是解此题的关键;本题的中点较多,除了运用等腰三角形三线合一的性质外,还多次运用了直角三角形斜边中线等于斜边一半的性质.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
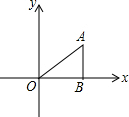 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )| A. | (-1,-$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$)或(-2,0) | C. | (-$\sqrt{3}$,1)或(0,-2) | D. | (-$\sqrt{3}$,1) |
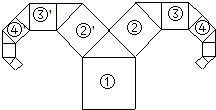 如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8.
如图所示为一种“羊头”形图案,其作法是从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②',…,依此类推,若正方形①的面积为64,则正方形④的面积为8. 用直尺、圆规作图,不写作法,但要保留作图痕迹.
用直尺、圆规作图,不写作法,但要保留作图痕迹.