题目内容
1.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
分析 首先根据勾股定理求出斜边AB的长,再根据三角形的面积为定值即可求出则点C到AB的距离.
解答 解:在Rt△ABC中,∠C=90°,则有AC2+BC2=AB2,
∵AC=9,BC=12,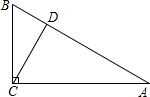
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=15,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h,
∴h=$\frac{12×9}{15}$=$\frac{36}{5}$=7.2.
故选A.
点评 本题考查了勾股定理在直角三角形中的应用,解本题的关键是正确的运用勾股定理,确定AB为斜边.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.电影院中座位数如表:
(1)写出表示第n排座位数an的代数式.
(2)写出表示前n排座位数Sn的代数式.
(3)如果电影院共有20排座位,那么该电影院一共有多少个座位?(Sn=a1+a2+…+an)
| 排数n | 每排座位数an |
| 1 | 20 |
| 2 | 22 |
| 3 | 24 |
| 4 | 26 |
| … | … |
(2)写出表示前n排座位数Sn的代数式.
(3)如果电影院共有20排座位,那么该电影院一共有多少个座位?(Sn=a1+a2+…+an)
16.下列运算中,正确的是( )
| A. | 3mn-3nm=0 | B. | 3x+3y=6xy | C. | 2a2+3a3=5a5 | D. | 7x-5x=2 |
13.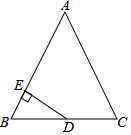 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )| A. | $\frac{10}{13}$ | B. | $\frac{15}{13}$ | C. | $\frac{45}{13}$ | D. | $\frac{60}{13}$ |
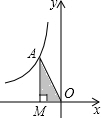 如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10.
如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10.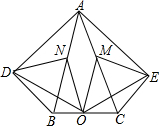 在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.