题目内容
3.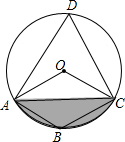 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )| A. | 4$π-3\sqrt{3}$ | B. | 4π$-6\sqrt{3}$ | C. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ | D. | 2$π-3\sqrt{3}$ |
分析 根据S阴=S扇形OAC-S△AOC,分别求出扇形、三角形的面积即可解决问题.
解答 解:作OE⊥AC垂足为E.
∵∠ABC=2∠D,∠ABC+∠D=180°,
∴∠D=60°,∠AOC=2∠D=120°,
在RT△AOE中,∵∠AEO=90°,∠OAC=∠OCA=30°,OA=2$\sqrt{3}$,
∴OE=$\sqrt{3}$,AE=3,AC=2AE=6,
∴S阴=S扇形OAC-S△AOC=$\frac{120π(2\sqrt{3})^{2}}{360}$-$\frac{1}{2}$•6•$\sqrt{3}$=4π-3$\sqrt{3}$.
故选A.
点评 本题考查扇形面积、三角形面积等知识,解题的关键是记住扇形的面积公式,三角形的面积公式,学会利用分割法求面积,属于中考常考题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
14.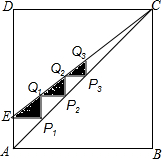 如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )
如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )
 如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )
如图.正方形ABCD的边长为4,点E为AD边上一点.,AE=1,连接AC,CE,过点E作AB的平行线交AC于点P1,过点P1作AD的平行线交CE于Q1,再过Q1作AB的平行线交AC于P2,…如此不断进行下去形成△AEP1,△P1Q1P2,△P2Q2P3,…,记它们的面积之和为S1,类似地形成△EP1Q1,△Q1P2Q2,△Q2P3Q3,…,记它们的面积之和为S2,则$\frac{{S}_{2}}{{S}_{1}}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
11.变量x,y有如下关系:①x+y=10;②y=$\frac{-5}{x}$;③y=|x-3|;④y2=8x,其中y是x的函数的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ① |
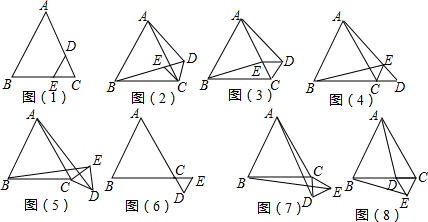
18.下列图中,不是轴对称图形的有( )个.


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.化简$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x | B. | x-1 | C. | -x | D. | x+1 |
15.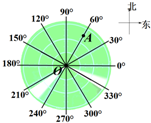 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
 一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )
一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为( )| A. | 事故船在搜救船的北偏东60°方向 | B. | 事故船在搜救船的北偏东30°方向 | ||
| C. | 事故船在搜救船的北偏西60°方向 | D. | 事故船在搜救船的南偏东30°方向 |
12.运用乘法公式计算(a+3)(a-3)的结果是( )
| A. | a2-6a+9 | B. | a2-3a+9 | C. | a2-9 | D. | a2-6a-9 |