题目内容
13.如图,△ABC和△CDE都是等边三角形,求证:AD=BE,②如果将△CDE绕C点沿顺时针方向旋转至如图(1)(2)(3)(4)(5)(6)(7)(8)的位置时,AD=BE还成立吗?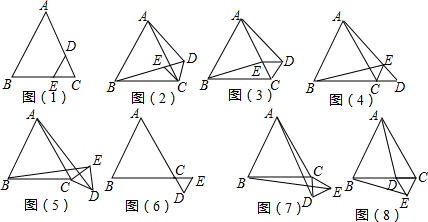
分析 根据等边三角形的性质得到∠ACB=∠DCE=60°,于是得到∠ACD=∠BCE,即可证明△ACD≌△BCE,根据全等三角形对应边相等的性质即可解题.
解答 解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,
∴AC-CD=BC-CE,
即AD=BE;
如图(2),
∵∠ACB=∠ECD=60°,
∴∠ACB-∠ACE=∠DCE-∠ACE,
即∠ACD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE;
同理将△CDE绕C点沿顺时针方向旋转至如图(3)(4)(5)(6)(7)(8)的位置时,AD=BE还成立.
点评 本题考查了旋转的性质,全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若方程组$\left\{{\begin{array}{l}{3x+5y=a+4}\\{2x+3y=a}\end{array}}\right.$的解x与y的和为3,则ax的值是( )
| A. | -42 | B. | 0 | C. | 7 | D. | 14 |
4. 如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
 如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )
如图,直线a,b分别与c相交,在标出的角∠2,∠3,∠4,∠5中,与∠1是同位角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
18.下列实数中,为无理数的是( )
| A. | $\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | 0.2 | D. | -7 |
2.在下列实数中,无理数是( )
| A. | sin45° | B. | $\frac{1}{3}$ | C. | 0.$\stackrel{•}{3}$ | D. | 3014 |
3.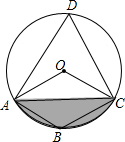 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC,若OC=2$\sqrt{3}$,则图中阴影部分的面积是( )| A. | 4$π-3\sqrt{3}$ | B. | 4π$-6\sqrt{3}$ | C. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ | D. | 2$π-3\sqrt{3}$ |