题目内容
17.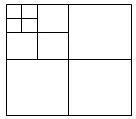 如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…
如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…(1)填表
| 剪的次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | 10 | 13 | … |
(3)若剪去10次,共剪出多少个小正方形?
(4)若原来正方形的边长为a,求当n=5时,所剪得的所有正方形的周长的和.
分析 (1)(2)由题意可知:每一次剪的时候,都是把上一次的图形中的一个进行剪切.所以在第一次4个的基础上,依次多3个,由此规律得出答案即可;
(3)把n=10,代入(2)中的规律求得答案即可;
(4)由题意可知,每一次剪得正方形的边长是上一次正方形边长的$\frac{1}{2}$,计算每一次所有正方形的周长和相加即可.
解答 解:(1)填表如下:
| 剪的次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | 10 | 13 | … |
(3)若剪去10次,共剪出3×10+1=31个小正方形;
(3)当n=5时,共16个图形,
边长$\frac{a}{2}$的正方形3个,边长$\frac{a}{2}$×$\frac{1}{2}$=$\frac{a}{4}$的正方形3个,边长$\frac{a}{4}$×$\frac{1}{2}$=$\frac{a}{8}$的正方形3个,边长$\frac{a}{8}$×$\frac{1}{2}$=$\frac{a}{16}$的正方形3个,边长$\frac{a}{16}$×$\frac{1}{2}$=$\frac{a}{32}$的正方形4个,
所有正方形的周长的和为:$\frac{a}{2}$×3+$\frac{a}{4}$×3+$\frac{a}{8}$×3+$\frac{a}{16}$×3+$\frac{a}{32}$×4=$\frac{47}{16}$a.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字的运算规律解决问题.

练习册系列答案
相关题目
7.单项式-$\frac{πa{b}^{3}{c}^{3}}{3}$的次数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{π}{3}$ | C. | 5 | D. | 6 |
5.我国科学家屠呦呦获得2015年诺贝尔医学奖,成为第一位获得诺贝尔科学奖项的本土中国科学家、第一位获得诺贝尔医学奖的华人科学奖.她的研究组第一个用乙醚提取青蒿素,并证实了青蒿素提物的高效抗疟作用,这一研究成果使全世界大约240000000人受益,用科学记数法将这个数据可表示为( )
| A. | 2.4×107 | B. | 24×107 | C. | 24×109 | D. | 2.4×108 |
6.已知a<0、b>0且|a|>|b|,则a、b、-a、-b的大小关系是( )
| A. | b>-a>a>-b | B. | -b>a>-a>b | C. | a>-b>-a>b | D. | -a>b>-b>a |
 如图,面积为60cm2的正方形的四个角是面积为3cm2的小正方形,求x的值.(精确到0.01cm)
如图,面积为60cm2的正方形的四个角是面积为3cm2的小正方形,求x的值.(精确到0.01cm) 把下列各数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来.-$\frac{1}{3}$,0,-3,0.2.
把下列各数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来.-$\frac{1}{3}$,0,-3,0.2. 如图,在钝角△ABC中.
如图,在钝角△ABC中.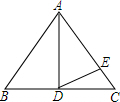 在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE.求∠CDE的度数.
在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE.求∠CDE的度数.