题目内容
11.从-3、-2、-1、1、2、3这六个数中,随机抽取一个数记作a,使关于x的分式方程$\frac{6}{2x-{x}^{2}}$-$\frac{a}{x-2}$=$\frac{1}{x}$有整数解,且使关于x的方程(a-1)x2-3x+2=0有实数解,则符合条件的所有a的和是( )| A. | -4 | B. | -1 | C. | 0 | D. | 1 |
分析 先求出满足分式方程条件存立时a的值,再求出方程(a-1)x2-3x+2=0有实数解时a的值,进而求出同时满足条件a的值.
解答 解:∵x的分式方程$\frac{6}{2x-{x}^{2}}$-$\frac{a}{x-2}$=$\frac{1}{x}$有整数解,
∴x=$\frac{-4}{a+1}$,
∵x是整数,
∴a=-3,-2,1,3;
∵分式方程$\frac{6}{2x-{x}^{2}}$-$\frac{a}{x-2}$=$\frac{1}{x}$有意义,
∴x≠0或2,
∴a≠-3,
∴a=-2,1,3,
∵于x的方程(a-1)x2-3x+2=0有实数解,
∴a=1或a<$\frac{17}{8}$,
∴使关于x的分式方程$\frac{6}{2x-{x}^{2}}$-$\frac{a}{x-2}$=$\frac{1}{x}$有整数解,且使关于x的方程(a-1)x2-3x+2=0有实数解a的值为-2或1,
符合条件的所有a的和是-2+1=-1,
故选B.
点评 本题主要考查了根的判别式以及分式方程的解的知识,解题的关键是掌握根的个数与系数的关系以及分式有意义的条件,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各组数中,能作为直角三角形三边长的是( )
| A. | 1,2,3 | B. | 4,5,6 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 6,8,10 |
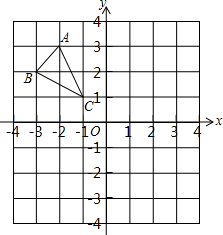 △ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移5个单位后再向下平移3个单位得到△A1B1C1
△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移5个单位后再向下平移3个单位得到△A1B1C1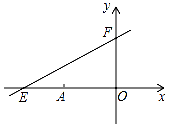 如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.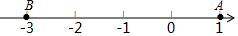 如图,已知数轴上两点A,B对应的数分别为1,-3,点P为数轴上一动点,点P以每秒0.5个单位的速度从O点向左运动,则经过4或10秒,使PA=3PB.
如图,已知数轴上两点A,B对应的数分别为1,-3,点P为数轴上一动点,点P以每秒0.5个单位的速度从O点向左运动,则经过4或10秒,使PA=3PB.