题目内容
19.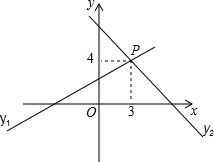 已知一次函数y1=kx+b与y2=mx+n的图象相交于P点(km≠0).
已知一次函数y1=kx+b与y2=mx+n的图象相交于P点(km≠0).(1)则方程组$\left\{\begin{array}{l}{kx+b=y}\\{mx+n=y}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$;
(2)当x=3时y1=y2,当x>3时y1>y2,当x<3时y1<y2.
分析 (1)直接根据函数图象交点坐标为两函数解析式组成的方程组的解进行回答;
(2)观察函数图象,它们交点的横坐标使y1=y2,写出一次函数y1=kx+b图象在y2=mx+n的图象上方所对应的自变量的范围可满足y1>y2,写出一次函数y1=kx+b图象在y2=mx+n的图象下方所对应的自变量的范围可满足y1<y2.
解答 解:(1)以为一次函数y1=kx+b与y2=mx+n的图象的交点P的坐标为(3,4),
所以方程组$\left\{\begin{array}{l}{kx+b=y}\\{mx+n=y}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$;
(2)当x=3时y1=y2,当x>3时y1>y2,当x<3时y1<y2.
故答案为$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$;x=3,x>3,x<3.
点评 本题考查了一次函数与二元一次方程(组):由于任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值;函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
10.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查奥运会100米决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查一个班级的学生对“中国好声音”节目的知晓率 | |
| C. | 调查金牛区中小学生每天课外体育锻炼的时间 | |
| D. | 调查“玉兔号”飞船各零部件的质量情况 |
7.A、B两地相距60千米,一辆汽车从A地去B地,则其平均速度x(千米/时)与行驶时间t(小时)之间的函数关系可表示为( )
| A. | x=-60t | B. | t=-60x | C. | x=$\frac{60}{t}$ | D. | t=-$\frac{60}{t}$ |
14.已知3x2-4x-2+□=2x2-x,□内应填( )
| A. | 5x2-3x-2 | B. | -x2+3x | C. | -x2+3x+2 | D. | -x2+3x-2 |
11.一次函数y=abx中,y随x的增大而增大,则关于x的方程ax2-2x-b=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 以上判断都不对 |
3.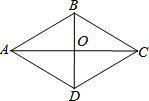 如图,在菱形ABCD中,∠DAB=60°,其中一条对角线BD的长为6,则菱形的边长是( )
如图,在菱形ABCD中,∠DAB=60°,其中一条对角线BD的长为6,则菱形的边长是( )
 如图,在菱形ABCD中,∠DAB=60°,其中一条对角线BD的长为6,则菱形的边长是( )
如图,在菱形ABCD中,∠DAB=60°,其中一条对角线BD的长为6,则菱形的边长是( )| A. | 10 | B. | 6 | C. | 3 | D. | 8 |
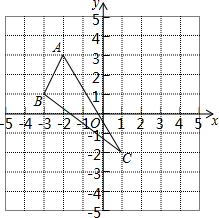 在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
在平面直角坐标系中,△ABC的三个顶点的位置如图所示.