题目内容
11.一次函数y=abx中,y随x的增大而增大,则关于x的方程ax2-2x-b=0的根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 以上判断都不对 |
分析 由函数y=abx中,y随x的增大而增大,根据一次函数的性质得到ab>0,则a≠0,可判断方程ax2-2x-b=0是一元二次方程,然后计算△,得到△=(-2)2-4•a•(-b)=4+4ab>0,根据△的意义得方程ax2-2x-b=0有两个不相等的实数根.
解答 解:∵一次函数y=abx中,y随x的增大而增大,
∴ab>0,
对于方程ax2-2x-b=0,
∵a≠0,
∴方程ax2-2x-b=0是一元二次方程,
∴△=(-2)2-4•a•(-b)=4+4ab>0,
∴方程ax2-2x-b=0有两个不相等的实数根,
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;△<0,方程没有实数根.也考查了反比例函数的性质以及一元二次方程根与系数的关系.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
6.运动员在10次百米赛跑训练中的成绩(单位:秒)如下表:
(1)这运动员10次赛跑成绩的中位数是10.8秒;众数是10.8秒.若达标绩为10.8秒,则该运动员百米赛跑的达标率为60%?
(2)试求该名运动员10次百米赛跑的平均成绩是多少?
| 成绩 | 10.7 | 10.8 | 10.9 | 11.0 | 11.2 |
| 次数 | 3 | 3 | 1 | 2 | 1 |
(2)试求该名运动员10次百米赛跑的平均成绩是多少?
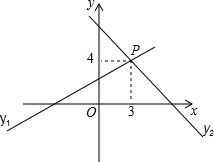 已知一次函数y1=kx+b与y2=mx+n的图象相交于P点(km≠0).
已知一次函数y1=kx+b与y2=mx+n的图象相交于P点(km≠0). 已知a、b所表示的数如图所示,下列结论正确的有②;(只填序号)
已知a、b所表示的数如图所示,下列结论正确的有②;(只填序号)